Полный напор для целого потока

Под «целым» потоком понимаем поток, имеющий поперечные сечения ко­нечных размеров.

По-прежнему рассматриваем только параллельноструйное и плавно изме­няющееся движения, т. е. случай, когда расчетные живые сечения плоские, причем будем пользоваться понятием средней скорости v.

Каждая элементарная струйка в данном живом сечении потока имеет (в общем случае) свой полный напор Н'_е, выражаемый зависимостью (3-65). Чтобы получить полный напор Н_е, являющийся гидродинамической характеристикой всего живого сечения, осредняем по плоскости живого сечения значения Н'_е, принадлежащие от­дельным струйкам. При этом рассуждаем следующим образом:

1) умножаем выражение (3-65) на вес жидкости, протекающей за время dt через живое сечение элементарной струйки 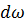, т. е. на величину 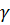dQdt; при этом получаем полную энергию этого веса жидкости;

2) интегрируем полученное выражение по всей плоскости живого сече­ния 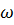; при этом получаем полную энергию объема Qdt жидкости, протекаю­щей за время dt через все живое сечение;

3) делим полученную энергию на вес указанного объема, т. е. на вели­чину yQdt, причем получаем меру энергии, отнесенную в среднем к единице веса жидкости, проходящей через данноеживое сечениеза время dt; эту величину мы и принимаем за полный напор Н_е, относящийся ко всему рассматриваемому живому сечению.

Следуя по такому пути и учитывая, что dQ =и 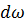, a Q = v 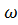можем написать:

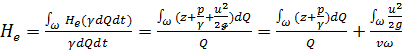(3-95)

или, сообразуясь с (3-72),

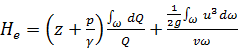(3-96)

учтя, наконец, (3-93), имеем:

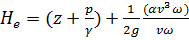(3-97)

что и приводит нас к окончательному выражению для Н_е:

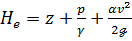(3-97)

Как видно, в случае целого потока скоростной напор, т. е. удельная кинетическая энергия, являющаяся мерой кинетической энергии, отнесенной в среднем к единице веса жидкости, находящейся в данном живом сечении, выражается через среднюю скорость v в виде:

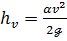(3-99)

где а — корректив кинетической энергии.

Что касается величины 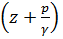,то она,как известно, представляет собой потенциальный напор, являющийся одинаковым (в данном плоском живом сечении) для всех элементарных струек, пересекающих это сечение (см. § 3-17).