Уравнение Бернулли для целого потока реальной

Будем рассматривать целый поток жидкости, ограниченный с боков водонепроницаемыми стенками русла, а также в случае безнапорного движе­ния еще и свободной поверхностью. Ставя такое условие, мы остановимся только на случае, когда через боковую поверхность потока отсутствует приток (или отток) жидкости, а также диффузия энергии (см. § 3-16).

Благодаря работе сил трения полная удельная энергия жидкости вдоль потока (вниз по течению) должна уменьшаться. Поэтому для реальной (вязкой) жидкости должны написать:

Н_е1>Н_е2, (3-100)

гдe Н_е1 и Н_е2 — полные напоры (полные удельные энергии) в живых сече­ниях: 1—1, взятом выше по течению, и 2—2, взятом ниже по течению.

Имея в виду соотношения (3-100) и (3-98), уравнение баланса энергии «уравнение Бернулли для целого потока) можем представить в виде (пред­полагая, чтоа₁ == a₂ = a₃):

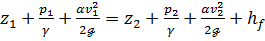(3-101)

h_f = H_ei — H_e, (3-102)

называется потерей напора; h_f есть полная энергия, теряемая всреднем единицей веса на пути от первого до второго сечения за счетработы внутренних и внешних сил трения.

Смысл величины h_f можно пояснить еще так:

1)«весовой расход» dQ элементарной струйки равен 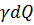; полная энергия, теряемая этим весом по пути от первого до второго сечения, равна 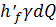, где h'_f — потеря напора для элементарной струйки;

2)полная энергия, теряемая всем расходом Q на пути от первого до второго сечения, рав­няется

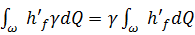(3-103)

3)отнеся эту энергию к единице веса жидкости, получаем

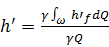(3-103)

Именно этой зависимостью величина h_f связана с величиной 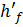Величина 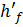различна для разных струек; величина h_f есть средняя среди величин h'_f, согласно формуле (3-104).

На рис. 3-25, аналогичном рис. 3-22, показаны пьезометрическая ли­лия р—р и напорная линия Е—Е для целого потока. Но вотличие от рис. 3-22 на рис. 3-25 напорная линия Е—Е оказывается негоризонт а л ь н о й. Эта линия понижается по течению, поскольку Н_е по течению убывает, причем величина снижения линии Е—Е на протяжении от живого сечения 1—1 до живого сечения 2—2 представляет собой величину потери напора h_f.

Элементарное снижение 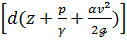напорной линии, отне­сенное к соответствующей элементарной длине ds, отмеренной по оси потока, называется гидравлическим уклоном и обозначается через J_e:

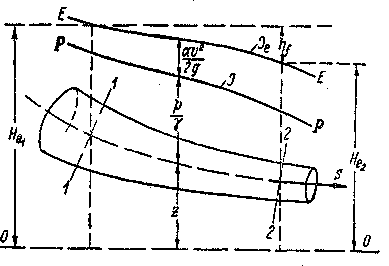
Рис. 3-25. Геометрическая интерпретация урав­нения Бернулли для целого потока реальной жидкости. 00 — плоскость сравнения, Р—Р — пьезоме­трическая линия, Е—Е — напорная линия, Не₁ и Не_г — полные напоры, hf — потеря на­пора, J — пьезометрический уклон, J_e — гид­равлический уклон

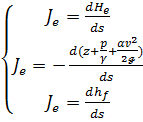(3-105)

Величина J_e, в общем случае переменная по длине потока, всегда положительна (при уста­новившемся движении): 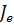> 0; только для случая идеальной жидкости J_e = 0. Понятие пьезо­метрического уклона в данном случае сохраняется полностью (см. § 3-14). Этот уклон в случае целого потока обозначается J и выражается зависимостью

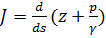(3-106)

Как видно, рис. 3-25 дает нам полную гидродинамическую картину:

а) фигура, заключенная между линией Р—Р и осью s потока, представляет
собой изменение величины вдоль потока;

б) фигура, заключенная между линиями; Р—Р и E—E,дает эпюру измене­
ния величины скоростного напора 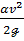; следовательно, эта фигура выражает

и характер изменения скорости v вдоль потока;

в) фигура, заключенная между линией Р—Р и плоскостью сравнения OO,
дает эпюру изменения потенциального напора вдоль потока;

г) фигура, заключенная между линией E—E и плоскостью сравнения OO,
представляет собой эпюру изменения полного напора вдоль потока.

Каждому живому сечению потока отвечает на рис. 3-25 вполне определен­ная точка линии Р—Р и вполне определенная точка линии Е—Е (точки линий Р—Р и Е—Е отвечают определенным живым сечениям, а не точкам живых сече­ний).

Уравнение Бернулли (3-101) выражает связь между гидродинамическими элементами двух живых сечений; оно как бы «связывает», соединяет два живых сечения 1—1 и 2—2 (из которых сечение 1—1 всегда расположено выше по течению сечения 2—2).

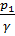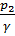Величины z₁и z₂, входящие в (3-101) представляют собой превышения над плоскостью сравнения ОО точек соответствующих живых сечений; величины и — пьезометрические высоты для этих точек. Естественно может возникнуть вопрос о том, какие именно точки живых сечений 1—1 и 2—2 следует рассматривать, когда мы соединяем эти сечения уравнением Бернулли. При построении пьезометрической линии Р—Р для целого потока, представляющей собой линию, проведенную по горизонтам жидкости в во­ображаемых пьезометрах, приключенных к разным живым сечениям, также может возникнуть вопрос о том, к каким именно точкам живых сечений сле­дует мысленно присоединить упомянутые пьезометры.

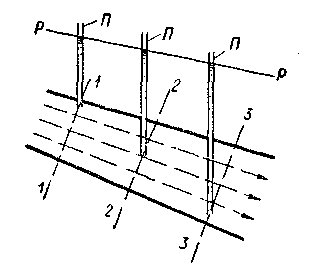
Ответ на этот вопрос вытекает из сказанного в § 3-17: так как для дан­ного живого сечения при плавно изменяющемся и параллельноструйном дви­жениях 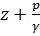= const, то безразлично, какие точки живых сечений будем рассматривать и к каким точкам этих сечений будем присоединять пьезо­метры; высотное положение точки линии Р—Р, отвечающей данному живому сечению, будем всегда одинаковым, какую бы точку этого сечения мы ни рассматривали. На рис. 3-26 показан поток; для построения линии Р—Р мы приключили здесь пьезометр в сечении 1—1 к самой верхней точке, в сече­нии 2—2 — к средней точке, в сечении 3—3 — к самой нижней точке живого сечения и т. д.

Из всего сказанного выше вытекают два основных условия применимости уравнения Бернулли (3-101) к потоку жидкости (эти два условия должны соблюдаться одновременно).

Рис. 3-26. К построению ли­нии Р—Р

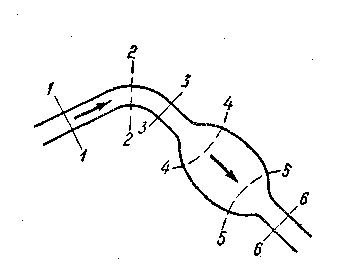
Рис. 3-27. Условия применения уравнения Бернулли

1-е условие. Движение жидкости должно быть установившимся, поскольку при выводе уравнения (3-60), положенного в основу уравнения (3-101), считали, что кинетическая энергия жидкости, заключенной в объеме между сечениями 1—1 и 2—2 (в пределах отсека А 'В, показанного на рис. 3-20) не изменяется во времени.[17]

2-е у с л о в и е. Движение жидкости в сечениях 1—1 и 2—2, соединяемых уравнением Бернулли, должно быть параллельноструйным или плавно изме­няющимся; в промежутке же между сечениями 1—1 и 2—2 движение жидкости может быть и резко изменяющимся. Это условие вытекает из следующих соображений. Если бы в сечениях 1—1 и 2—2 движение было резко изме­няющимся (расчетные живые сечения 1—1 и 2—2 были бы криволинейными),

то для этих сечений не имели бы условия 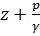= const. Такое положение

не позволило бы нам получить выражение (3-98) для полного напора H_e и, следовательно, писать неравенство (3-100).

Что касается промежутка между сечениями 1—1 и 2—2, то обстоя­тельства движения на длине этого промежутка непосредственно учитываются в уравнении Бернулли (3-101) только членом h_f. Если мы имеем возможность определить h_f для участка резко изменяющегося движения (см. гл. 4),^2[18] то наличие такого участка не может препятствовать применению уравнения Бернулли.

На рис. 3-27 представлен поток, имеющий участки плавно изменяющегося движения (на этих участках живые сечения показаны сплошными линиями) и участки резко изменяющегося движения (где живые сечения показаны штриховыми линиями). Очевидно, уравнением Бернулли можно соединять между собой сечения 1 и 3, 3 и 6 и т. д.; соединять же, например, сечения 1 и 2 или 2 и 4 и т. д. уравнением Бернулли нельзя.