Материалы практических занятий по вопросам, связанным с использованием уравнения Бернулли

1°. Общая схема применения уравнения Бернулли.Уравнение Бернулли удобно при­менять, следуя такой схеме:

1) устанавливаем два сечения, которые будем соединять уравнением Бернулли. Здесь надо намечать такие сечения, для которых известно возможно большее число гидродинами­ческих элементов. Если потребуется найти тот или другой гидродинамический элемент для какого-либо живого сечения, то это живое сечение должно быть включено в число двух сече­ний, соединяемых уравнением Бернулли;

2) намечаем горизонтальную плоскость сравнения. Часто эту плоскость удобно назна­чать так, чтобы z₁или z₂ входящее в уравнение Бернулли, обратилось в нуль;

3) пишем уравнение Бернулли в полном виде, как оно было нами получено, см. , 3-101);

4) устанавливаем значения отдельных слагаемых, входящих в это уравнение;

5) подставляем найденные выражения для отдельных слагаемых в уравнение Бернулли и производим необходимые преобразования.

2°. Задачи. № 1.На рис. 3-31 представлен сосуд, от которого отходит труба. Исте­чение жидкости из трубы происходит в атмосферу. Предполагаем, что движение жидкости в трубе — установившееся, потерями напора можно пренебречь.

Дано: z₁= 4 м; z₂ = 2 м; z₁ = 0,5 ж; z₁= 0; 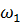= 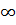; 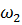= 0,015м^г 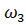= 0,04м²; 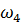= 0,02 м², где z и 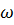(площади живых сечений) показаны на чертеже.

Требуется найти: а) расход Q жидкости, вытекающей из трубы; б) давления и ско­рости в сечениях, указанных на чертеже.

Примечания. 1. Скоростью v₁ движения жидкости в сосуде (в сечении 1—1) обычно пренебрегают ввиду ее малости. 2. При решении этой задачи, помимо уравнения Бернулли, следует пользоваться уравнением неразрывности.

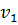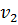Ответ: Q = 177,2л/сек; = 0; = 11,80 м/сек; 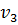= 4,43 м/сек; 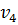⁼ 8,86 м/сек;

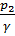=-5,1 м; 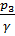=2,5«; - 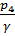= 0.

№ 2. На рис. 3-32 показан водомер Вентури, представляющий собой местное сужение, созданное на круглом трубопроводе.

Дано (обозначения см. на чертеже): а = 1,0 м; 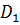=0,1 м; D₂ = 0,05 м. Требуется найти расход Q в трубе, пренебрегая потерями напора( 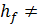0) и считая дви­жение жидкости установившимся. Ответ: Q = 9,0 л/сек.

3°. Построение напорной и пьезометрической линий. Рассмотрим трубопровод, соеди­няющий два сосуда А и В (рис. 3-33), наполненные жидкостью. Будем считать, что в трубо­проводе имеет место установившееся движение, а следовательно, расход Q в трубопроводе во времени не изменяется. Ставя так вопрос, надо при этом предполагать, что расходы жидко­сти, подаваемой в сосуд А и удаляемой из сосуда 5, одинаковы. При этом уровни жидкости в сосудах Л и В все время будут поддерживаться на одной и той же высоте.

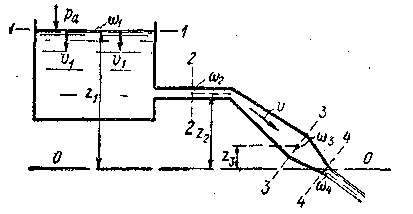
Рис. 3-31. К задаче № 1, п. 2°

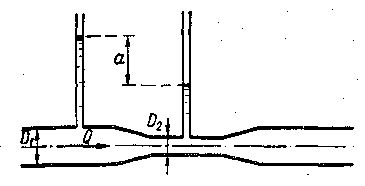
Рис. 3-32. К задаче № 2, а. 2°

Поскольку поперечное (горизонтальное) сечение сосудов А и В велико сравнительно с поперечным сечением трубопровода, считаем:

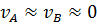
Так как сосуды А и В открыты, то на поверхность жидкости в них действует атмо­сферное давление р_а. Однако мы не будем учитывать это давление, понимая в уравнении Бернулли под величиной⁵ пьезометрическую высоту, отвечающую избыточному давлению (см. конец § 3-14).

Наметим плоскость сравнения OO, а также несколько точек (1, 2, 3, . . .) в сосуде А.

Для этих точек величины z и величины будут различны. Однако сумма величин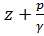

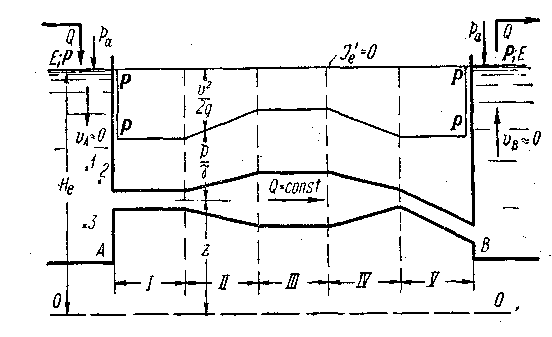
Рис. 3-33. Пьезометрическая линия Р—Р для участков тру­бопровода разного вида (случай идеальной жидкости)

будет постоянна. Скоростной напор в этих точках пренебрежимо мал. Ясно, что полный на­пор Н_е для всех точек жидкости в сосуде равен потенциальному напору Н:

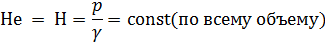
Отсюда получаем следующий общий вывод: для жидкости в сосуде напорная и пьезо­метрическая линии совпадают и располагаются на уровне горизонта жидкости в сосуде.

Переходя к построению линий Е—Е и Р—Р для трубопровода, ограничимся рассмотре­нием только идеальной жидкости. Так как потеря напора в случае такой жидкости отсут­ствует, то можем утверждать, что напоры в сосудах А и В будут одинаковы, а следовательно, горизонты жидкости в сосудах А и В будут находиться на одном уровне

(несмотря на наличие движения жидкости в трубопроводе).¹[19]

Как известно, напорная линия Е—Е в случае идеальной жидкости представляет собой горизонтальную прямую. Эту прямую, прежде чем обратиться к построению линии Р—P, мы и проводим на чертеже (на уровне горизонтов воды в сосудах). Далее вниз от прямой

Е—Е откладываем соответствующие скоростные напоры 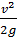(коэффициент 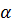считаем 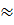1,0)

и получаем линию Р—Р—Р—Р.

Анализируя характер изменения скорости, а следовательно, и скоростного напора вдоль трубопровода, можно сделать следующие замечания в отношении линии Р—Р:

а) если поток расширяется (см. участок II трубопровода), то скорость и скоростной
напор вдоль трубопровода уменьшаются. Поэтому для расширяющегося трубопровода ли­ния Р—Р вдоль потока должна подниматься. В этом случае на длине рассматриваемого
участка кинетическая энергия потока частично переходит в потенциальную;

б) если поток сужается (см. участок IV трубопровода), получаем обратную картину;

в) если поток цилиндрический (о = const; см. участки /, /// и К трубопровода),
то линия Р—Р оказывается прямой, параллельной Е—Е, т. е. в случае идеальной

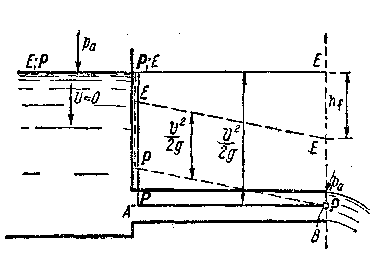
Рис. 3-.34. Истечение в атмосферу из цилин­дрической трубы (случаи идеальной и ре­альной жидкостей)

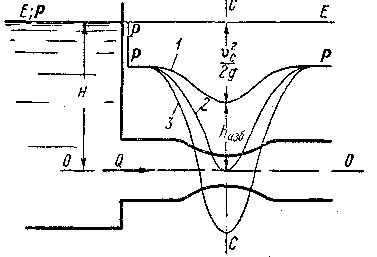
Рис. 3-35. Возникновение вакуума при су­жении трубы

жидкости для цилиндрических трубопроводов линия Р—Р получается всегда в виде гори­зонтальной прямой (или линии, лежащей в горизонтальной плоскости);

г) при изменении высотного положения рассматриваемого трубопровода высотное
положение линий Е—Е и Р—Р не должно изменяться (см. участок V);

д) от положения плоскости сравнения 00 высотное положение линий Е—Е и Р—Р,
разумеется, вовсе не зависит. Однако от высотного положения плоскости 00 зависит вели­
чина полного напора Н_е.

Рассмотрим теперь два особых случая.

1. Случай истечения жидкости в атмосферу (рис. 3-34). При исте­чении в атмосферу в точке В будем иметь атмосферное давление, которое обычно не учитывают (см. выше). Избыточное давление в точке В равно нулю. Превышение пьезометрической линии над осью трубы, как известно, выражает давление в трубе. Если избыточное давление в точке В равно нулю, то можем утверждать, что пьезометрическая линия должна про­ходить через эту точку.

Следует запомнить правило: при истечении в атмосферу пьезометрическая линия проходит через центр выходного сечения (если при построении линии Р—Р мы оперируем избыточным давлением).

На рис. 3-34 сплошными линиями показаны линии Е—Е и Р—Р—Р, относящиеся к слу­чаю идеальной жидкости, и штриховыми линиями — те же линии, относящиеся к случаю реальной жидкости. Как видно, скоростной напор, а следовательно, и скорость в случае реальной жидкости получаются меньшими, чем в случае идеальной жидкости.

3.Случай местного сужения трубы; вакуум. Представим на рис. 3-35 горизонтальную трубу, имеющую местное сужение. Ограничимся рассмотрением только идеальной жидкости, причем будем считать, что течение в трубе направлено слева направо и расход воды в трубе равен Q.

Обозначим через Н полный напор Н_е в сосуде (относительно плоскости сравнения 00, показанной на чертеже).

Пьезометрическая высота 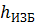(отвечающая избыточному давлению) в сече­нии СС, где имеется местное сужение (см. пьезометрическую линию 1),

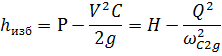
где 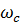— площадь живого сечения по линии СС; v_r— скорость в этом сечении.

Будем считать величины H и Q нам заданы: Н = const и Q = const При этом условии представим себе что 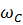постепенно уменьшаетс я. Очевидно, в случае, когда окажется что

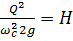т.е.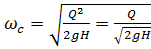

величина 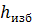обратится в нуль, и пьезо­метрическая линия примет положение 2. В случае же

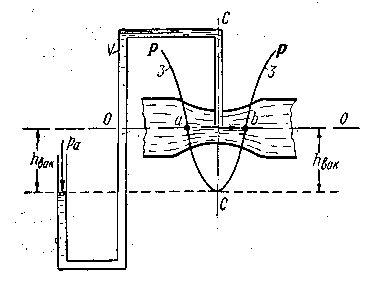
Рис. 3-36. Измерение вакуума в месте сужения трубы

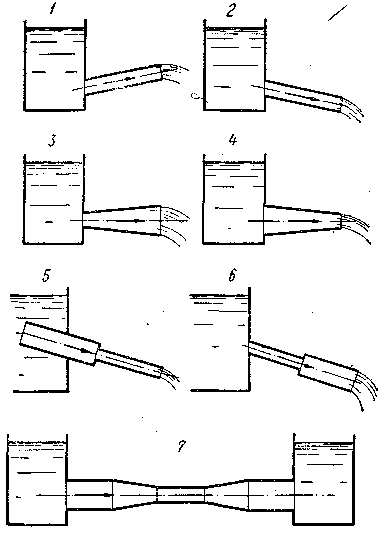
Рис. 3-37. К задачам п. 4°

получим отрицательное значение пьезометрической высоты 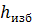, отвечающей избыточному давлению, причем пьезометрическая линия займет положение 3: на некоторой длине трубы линия Р—Р будет располагаться ниже оси трубы. Легко видеть, что на этой длине в трубе будет иметь место вакуум.

Необходимо запомнить следующее правило: если линия Р—Р располагается выше оси трубы, то в трубе имеется давление больше атмосферного, причем превышение этой линии над осью трубы выражает избыточное давление в трубе; если же линия Р—Р располагается ниже оси трубы, то в трубе имеет место вакуум, причем превышение оси трубы над ли­нией Р—Р выражает величину этого вакуума.[20]

Величина такого вакуума может быть измерена вакуумметром (рис. 3-36).

Разумеется, в случае пьезометрической линии 2 (рис. 3-35) в центре сечения СС будет атмосферное давление; в точках а и b на рис. 3-36, где линия Р—Р пересекает ось трубы, также будет иметь место атмосферное давление.

Известно (см. § 1-5), что в случае снижения давления (при постоянной температуре) из жидкости выделяется растворенный в ней воздух (газ); кроме того, при достаточно большом снижении давления (при большом вакууме) возникает явление кавитации.

Эти явления в случаях, подобных представленным на рис. 3-35 и 3-36, обусловливают следующее (см. § 1-5):

а) Давление в жидкости на участке трубы аb (рис. 3-36) не может снизиться ниже давле­ния р_н._п. насыщенных паров жидкости (при данной температуре): с уменьшением сое объем паровоздушной области (области разрывов) будет расти; давление же в жидкости практически будет оставаться равным р_н. _п. Это абсолютное давление будет отвечать предельному вакууму 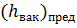т. е. такому вакууму, больше которого невозможно получить для данной жидкости при данной ее температуре.

б) При некотором вакууме, несколько меньшем 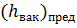развивающаяся кавитация
может вызывать, например, опасную эрозию стенок трубопровода. В этом случае вакуум
в трубе недопустимо увеличивать выше некоторой величины , называемой допу­стимым вакуумом (по условиям кавитации).

в) При наличии разрывов в жидкости, нарушающих сплошность ее движения, особенно
в случаях, когда объем этих разрывов изменяется во времени, уравнение Бернулли и урав­нение баланса расхода, полученные для сплошной среды, могут оказаться неприемлемыми для
анализа движения жидкости в суженном месте трубопровода.

4°. Задачи. Построить линии Е—Е и Р—Р для схем, представленных на рис. 3-37 в пред­положении, что жидкость идеальная. При этом следует:

а) отметить случаи наличия вакуума (и его наибольшую величину);

б) показать величины напоров Н_е для нескольких сечений при различных положениях
плоскости сравнения;

в) рассмотреть вопрос о том, как должны изменяться линии Е—Е и Р—Р при переходе от идеальной жидкости к реальной.