Два режима движения реальной жидкости

Рядом исследователей (Хагеном — в 1839 г. и 1854 г., Д. И. Менделее­вым— в 1880 г.) было замечено, что существует два принципиально разных режима движения жидкости. Наиболее полно этот вопрос иссле­довал в 1883 г. английский физик О. Рейнольде.

Представим на рис. 3-40 сосуд Л, наполненный какой-либо жидкостью; от этого сосуда отходит труба Т с прозрачными стенками, имеющая на конце кран К. Над сосудом А располагается бачок с краской, от которого краска при помощи тонкой трубки подводится к входному сечению трубы Т. Откры­вая или закрывая кран К, изменяем величину расхода Q жидкости в трубе, а следовательно, и величину средней скорости v = Q : .

В результате таких опытов было установлено следующее. 1. При скоростях v в трубе, меньших некоторой скорости v_K:

v< v_K (3-126’)

краска, попадающая в трубу Т (рис. 3-40), окрашивает только одну струйку потока. Если к входному сечению трубы Т приключить вторую трубку, подводящую краску (см. рис. 3-41 а, на котором изображена деталь В, указанная на рис. 3-40), то при этом окрасится вторая струйка по­тока и т. д.

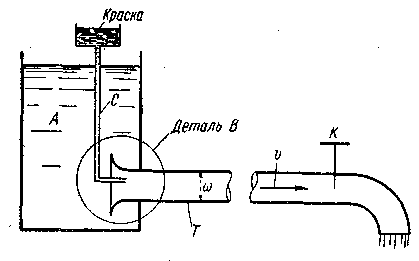
Рис. 3-40. Схема прибора Рейнольдса

2. При скоростях v в трубе, больших v_K:

v>v_K (3-126")

вся жидкость, находящаяся в трубе, окрашивается по всему своему объему (рис. 3-41, б). Здесь жидкость в целом имеет поступа­тельное движение слева направо, вместе с тем все составляющие ее частицы перемещаются по слу­чайным неопределенно искривлен­ным траекториям, имеющим пространственную форму; при этом движе­нии траектории частиц, проходящие в разные моменты времени через непо­движную точку пространства, имеют различный вид (занимают разное положение в пространстве и имеют различную форму); данное движение носит беспорядочный хаотический характер и

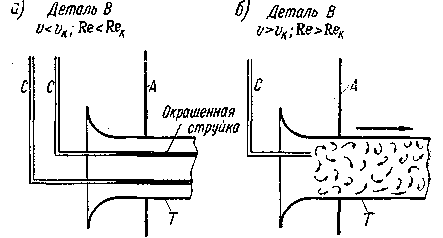
Рис. 3-41. Режимы движения: ламинарный (схема о) и турбулентный (схема б)

сопровождается постоянным перемешиванием жид­кости. Движение жидкости, пока­занное на рис. 3-41, а, получающееся при условии (3-126'), на­зывается ламинарным движением. Здесь частицы жидкости движутся по траекто­риям, параллельным стенкам трубы, без перемешивания.

Движение жидкости, пока­занное на рис 3-41, б, полу­чающееся при условии (3-126"), называется турбулент­ным движением. Здесь имеет место перемешивание жидкости.[22]

Скорость v_K, входящая в соотношения (3-126') и (3-126"), при которой тур­булентный режим (при уменьшении скоростей в трубе[23]) переходит в ламинар­ный режим движения жидкости, называется критической скоро­стью.

О. Рейнольде на основании приближенных теоретических рассуждений, проверенных в дальнейшем опытами, получил следующую формулу[24] для v_K:

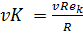(3-127)

где R — гидравлический радиус; v — так называемый кинематичес­кий коэффициент вязкости жидкости:

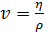(3-128)

здесь 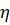— так называемый динамический коэффициент вязкости жидкости (см. ниже § 4-3); Re_K — безразмерный эмпиричес­кий коэффициент, называемый критическим числом Рей-ноль д с а.

О. Рейнольде дал приближенный вывод зависимости (3-127), основанный на использо­вании особого метода, называемого методом размерностей.

Предположив, что v_K зависит только от трех величин: р, ц и D, можно написать за­висимость для v_K в следующем виде:

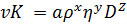(A)

где а — неизвестный постоянный безразмерный коэффициент; х, у, z— неизвестные пока­затели степени.

Размерность величин, входящих в (А), следующая:

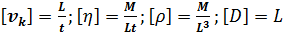(Б)

где L, t, M — символы соответственно длины, времени и массы (см. § 4-3). Учитывая (Б), зависимость (А) можно представить в форме:

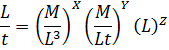
что и приводится к виду

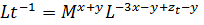(Г)

Чтобы эта зависимость имела смысл, показатели степени при М, L, i в правой и левой частях ее должны быть одинаковыми:

x+y=0; -3-y+z-1; -y=1

х= —1; у= +1; z= —1.

Подставляя эти значения х, у, z в зависимость (А) и заменяя обозначение а безразмер­ной величиной 4Re_K, а диаметр трубы D гидравлическим радиусом R = D/4, мы и получав!: формулу для v_K.

Безразмерный эмпирический коэффициент Re_K (критическое число Рей-нольдса), входящий в формулу (3-127), как показывают опыты, равен:

а) для круглоцилиндрических напорных труб, согласно экспериментам
Рейнольдса (в трактовке их Н. Н. Павловским):

; (3-129)

согласно же данным некоторых других авторов число Re_K для круглоцилин­дрических труб имеет значительно меньшую величину;

б) для безнапорных цилиндрических каналов широкого прямоугольного
сечения, по данным Хопфа,¹

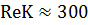. (3-130)

При обычно встречающейся шероховатости стенок труб величину Re_K принято считать от нее не зависящей. В случае цилиндрических достаточно длинных потоков величина Re_K оказывается зависящей только от формы поперечного сечения потока.

¹ В литературе приводятся и другие значения для этого числа (по данным А. П. Зегжда,Re_K= 900-=-1000).

² На величину Re_K в значительной мере влияет степень отклонения формы потока о:
цилиндрической. В случае сужающихся по длине потоков ламинарное движение при увели­чении скоростей переходит в турбулентное позже, чем в случае расширяющихся по длине
потоков (при одинаковых прочих условиях).

Формулу (3-127) можно представить в виде:

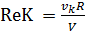(3-131)

Введем новое обозначение:

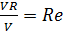(3-132)

где v — действительная (а не критическая) средняя скорость.

Умножим затем неравенства (3-126') и (3-126") на постоянное для данного потока число (R : v). Тогда, учтя выражения (3-131) и (3-132), условия существования того или другого режима движе­ния жидкости можем переписать в виде:

1) если

Re < Re_K, (3-133)

то должен иметь место ламинарный режим,

2) если

Re > Re_K (3-134)

то должен иметь место турбулентный режим.

Безразмерная величина Re, выражаемая согласно (3-132), через среднюю скорость v (вычисленную для действительного потока), называется числом Рейнольдса. Не следует смешивать понятий: числа Рейнольдса Re и критического числа Рейнольдса Re_K. Соот­ношениями (3-133) и (3-134) пользоваться удобнее, чем соотношениями (3-126') и (3-126"), поскольку безразмерная величина Re_K является постоян­ной для потока заданной геометрической формы; величина же v_K зависит еще от свойств жидкости (что учитывается коэффициентом v), а также от размеров потока.

В заключение приведем следующие отдельные замечания.

1. При изучении напорного движения жидкости в круглых трубах
число Рейнольдса обычно выражают не через гидравлический радиус, что
мы имели выше, а через диаметр т р у б ы D. Такое число Рейнольдса,
учтя (3-54), можно представить в виде:

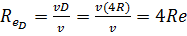(3-135)

Пользуясь вместо Re величиной 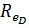, получаем, согласно Н. Н. Павлов­скому, [см. (3-129)], что

.

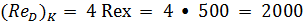Некоторые другие авторы полагают, что (Re_D)_K приближается или к 1000, или к 2300. Имея в виду такое положение, далее будем считать, что критическое число Рейнольдса (Re_D)_K лежит в пределах от 1000 до 2300:

(Re_D)_K = 1000 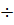2300 (3-136)

2. В гидротехнической практике обычно сталкиваемся с турбулентным движением. Движение воды в трубах, каналах, реках, как правило, является турбулентным. Имеется только один часто встречающийся в гидротехнике случай ламинарного движения — это движение грунтовой воды (воды, просачивающейся через поры грунта). В области же других специальностей, где имеют дело с движением особенно вязких жидкостей (масел и т. п.), ламинарный режим может встречаться достаточно часто.

3. Необходимо особенно подчеркнуть, что приведенные ранее основные уравнения гидродинамики (уравнение неразрывности, уравнение Бернулли и гидравлическое уравнение количества движения) применимы как к ламинарному, так и к турбулентному движению.

При этом, однако, в частности величина потерь напора h_f, входящая в урав­нение Бернулли, в случае турбулентного и в случае ламинарного потока выражается различными зависимостями. Далее (в гл. 4) будут приве­дены эти зависимости, а также пояснен вопрос о том, каким образом «бес­порядочное», турбулентное движение жидкости (рис. 3-41, б) для расчета заменяется той «струйчатой моделью», которую рассматривали ранее (в пред­шествующих параграфах).

4. При выполнении соответствующих опытов (рис. 3-40), оградив опыт­ную установку от возможных сотрясений, обеспечив плавный вход жидкости в трубу и т. п.-, мы можем, постепенно увеличивая скорости v в трубе Т,

Рис. 3-42. Переход ламинарного режима (ЛР) в турбулентный (ТР) и переход турбулентного режима в ламинарный. 1 — зона ламинарного режима; 2 — зона турбулент­ного режима; 3 .— неустойчивая или переходная зона

затянуть» существование ламинар­ного режима до некоторой ско­рости v'_K, где v'_K > v_K. Однако ламинарный режим при соотно­шениях v_K < v < v'_K является неустойчивым: в этом слу­чае при малейшем возмущении потока (например, при сотрясении трубы Г) ламинарный режим мо­жет «разрушиться» и перейти в турбулентный. Скорость v'_K иногда называют верхней крити­ческой скоростью. Ве­личина ее неопределенна (зави­сит от условий проведения опы­тов).

Если при v > v_K мы можем хотя бы в искусственной обста­новке опыта получить ламинарный режим, то при v < v_K турбулентный режим ни при каких условиях получен быть не может.

Поясним сказанное выше при помощи рис. 3-42. На этом рисунке пока­зана ось скоростей v. Если мы движемся по этой оси вверх (увеличивая ско­рость и), то ламинарный режим (ЛР) переходит в турбулентный режим (ТР) при скорости v'_K; если же спускаемся по этой оси вниз, то турбулентный режим переходит в ламинарный при скорости v_K, причем скорость v_K можно здесь назвать нижней критической скоростью.

Область скоростей v_K < v < v'_K называют неустойчивой или переходной зоной.

В соответствии со сказанным о скоростях v_K и v'_K следует различать нижнее число Рейнольдса Re_K в частности(Re_D)_K; [см. (3-136)] и верх­нее число Рейнольдса Re_K', выражаемое через скорость v'_K. При практи­ческих расчетах всегда полагают, что в переходной зоне имеет место турбу­лентный режим.

[1] В дальнейшем в случаях, когда под величиной р понимают как гидростатическое, гак и гидродинамическое давление, данную величину р будем именовать гидромеха­ническим давлением.

[2] В соответствующих местах уравнений (3-20) порядок расстановки букв х, у, г выдержан согласно так называемой круговой последовательности (х, у, z, х, у, z, . . .): 1) x, у, z; 2) у, z, х; 3) z, х, у. В скобках уравнения (3-20) заключены, как иногда говоря: «накрест взятые производные»

[3] Термин «медленно изменяющееся» движение ранее применялся в ином смысле: так называли движение, именуемое нами «плавно изменяющимся» (стр. 68).

[4] Под элементарной площадкой понимаем весьма малую площадку, удовлетво­ряющую условиям: координаты z ее точек отличаются друг от друга на бесконечно малую величину; это же условие должно удовлетворяться и для координат х и у, а также для ве­личин рай.

[5] В теоретической гидромеханике термину «струйка» приписывают иногда несколько иной смысл.

[6] Иногда в литературе плавно изменяющееся движение называют медленно изменяю­щимся (см. сноску на стр. 66).

[7] Существуют системы кривых, к которым нельзя провести ортогональную поверхность. Такого рода системы линий тока рассматривать здесь не будем.

[8] Можно, однако, представить себе частный случай плавно и резко изменяющихся дви­жений, когда и в этом случае живые сечения будут строго плоскими (случай движения в трубе, изогнутой по окружности).

[9] Понятие элементарного объема (параллелепипеда) определяется аналогично понятию элементарной площадки

[10] Один частный случай не прямолинейного равномерного движения (не имею­щий практического значения), отмеченный в сноске 3 на стр. 68, как здесь, так и ниже, исключаем из рассмотрения, считая равномерное движение всегда прямолиней­ным.

[11] С 7-й классификацией движений (т. е. физических явлений) не следует смешивать классификацию математических задач: «задача трехмерная», «задача двухмерная», «задача одномерная». Здесь имеется в виду зависимость того или другого параметра потока (скорости, давления) соответственно от трех, двух или одной координаты пространства. Для заданного случая движения жидкости та или другая математическая задача из названных выше часто получается в зависимости от принятой системы координат. Например, решение вопроса об осесимметричном движении при использовании прямо­угольной системы декартовых координат может привести нас к трехмерной задаче; при использовании в этом же случае полярной системы координат — к двухмерной (а иногда и к одномерной) задаче.

[12] Иногда «трубкой Пито» называют измерительное устройство (прибор), состоящее из двух трубок П₁ и П₂.

[13] Значком «прим» (') обозначаются (как здесь, так и ниже) величины, относящиеся к элементарной струйке.

[14] Доказательство этого положения аналогично доказательству положения (3-84).

[15] Эти численные значения 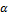и 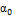имеют место в случае так называемого турбулентного режима движения жидкости (см. § 3-23).

[16] Данное уравнение принято называть уравнением Бернулли. Однако Д. Бернулли
получил только уравнение (3-60), приведенное в § 3-12 (для случая установившегося движения
идеальной жидкости, подверженной действию только сил тяжести). Уравнения, описываемые
в настоящем параграфе и в § 3-16 (а также приводимые далее в гл. 9 для случая неустано­
вившегося движения), были составлены в дальнейшем на основании как работ Д. Бернулли,
так и работ других авторов (Эйлера, Кориолиса, Буссинеска и др.).

[17] В гл. 9 будет получено уравнение Бернулли, относящееся к неустановившемуся
движению (§ 9-2; 9-3; 9-4).

[18] В этой главе рассматриваются способы определения величин потерь напора h_f.

[19] В случае движения в трубе реальной жидкости уровень ее в сосуде В должен рас­полагаться ниже уровня жидкости в сосуде А; при этом линия Е—Е получает некоторый наклон в сторону сосуда В. Если бы мы не пренебрегали скоростями v_A и v_B и считали v_A ≠ v_B то и в случае идеальной жидкости имели бы разность уровней в сосудах Л и В,

равную причем величина 0 определялась бы однозначно по этой разности уровней (и площадям горизонтальных сечений сосудов А и В).

[20] Имеется в виду линия Р—Р, построенная для избыточного давления.

[21] Имеется в виду только случай движения тела в направлении действия силы Р_х

[22] Слово «ламинарный» происходит от латинского слова, означающего «слоистый». Слово турбулентный» происходит также от латинского слова, означающего «беспорядочный».

[23] При увеличении скоростей и в трубе Т (когда ламинарный режим переходит в тур­булентный) значение v_K получается иное (см. конец настоящего параграфа).

[24] О. Рейнольдс, собственно, рассматривал только круглые трубы и вместо гидравли­ческого радиуса, входящего в (3-127), использовал диаметр трубы D = AR.