Сила лобового сопротивления твердого тела, частично или полностью погруженного в движущуюся жидкость

В п. 4°, § 3-22 был освещен пример так называемой внешней задачи (см. § 3-1). Ниже рассмотрим еще один такой пример.

Предположим, что твердое тело (полностью или частично погруженное в установив­шийся поток жидкости) совершает равномерное прямолинейное движение в направлении при­ложенной к нему внешней силы Р_х.

Будем считать, что направление силы Р_х, а следовательно, и направление движения тела, нам заданы. Вдоль этого заданного направления наметим ось х.

При подходе к телу (в достаточном удалении от него) наметим также живое сечение потока, причем через и₀ обозначим скорости, отвечающие этому «подходному сечению»; дополнительно будем считать, что скорости и₀ распределяются примерно равномерно по подходному живому сечению (и₀₌const). Направление и величину скоростей и₀ следует считать заданными.

В общем случае направление скоростей и_а и направление сил Р_х не совпадают. На рассматриваемое твердое тело, помимо собственного веса и механического воздействия жидко­сти, могут действовать и другие внешние силы.

Рассмотрим поверхность твердого тела, омываемую жидкостью. К элементарным площадкам, составляющим эту поверхность, со стороны жидкости приложены: а) элементарные нормальные силы гидродинамического давления и б) элементарные касательные силы трения.

Представим себе главный вектор упомянутых элементарных сил (давления и трения), причем разложим этот вектор на два направления: а) на известное нам направление оси х; полученную при этом составляющую обозначим через R_x иб) на направление, нормальное к оси х; эту вторую составляющую обозначим через R_z.

Силу R_z, если она оказывается направленной вертикально вверх, именуют подъ­емной силой.

Сила R_x направлена в сторону противоположную движению тела.[21] Именно эту силу и называют лобовым сопротивлением. Как видно, сила лобового сопротивления твердого тела (движущегося равномерно и прямолинейно в установившемся потоке) представляет собой проек­цию упомянутого главного вектора на направление движения тела.

Величину силы R_x для твердого тела произвольной формы приходится определять по эмпирической формуле:

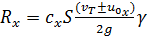(3-125)

где 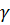— удельный вес жидкости; 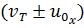— скорость движения жидкости относительно тела, причем здесь 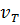— абсолютная скорость движения тела и и_0х — проекция скорости и₀ на ось х; S — площадь проекции тела (или его части, погруженной в жидкость) на пло­скость, нормальную к оси х, т. е. к направлению движения тела; с_х — эмпирический безраз­мерный коэффициент, который может быть назван коэффициентом лобового сопротивления.

Для так называемой квадратичной области сопротивления (см. далее § 4-10) вели­чина с_х зависит только от формы тела и шероховатости его поверхности, а также от поло­жения (от ориентировки) этого тела в потоке. В справочной литературе приводятся соответ­ствующие численные значения коэффициента с_х

По формуле (3-125), разумеется, можно определить силу 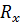и для покоящегося тела (тела неподвижно закрепленного), обтекаемого жидкостью.

Необходимо отметить, что для тел простейшей геометрической формы (шара, цилиндра и т. п.) формула (3-125) может быть обоснована теоретически, причем для величины с_х могут быть получены (для некоторых случаев движения жидкости) соответствующие прибли­женные теоретические зависимости.