Протекающей через данное живое сечение

(второе вспомогательное положение)

Рассмотрим две разные схемы потока, имеющего плоские живые сечения: с х е м у а (рис. 3-24),на которой изображен продольный разрез действи­тельного потока, характеризуемого неравномерным распределением скоростей по живому сечению АВ, и с х е м у б (рис. 3-24), на которой изо­бражен продольный разрез соответствующего расчетного (услов­ного) потока, характеризуемого тем обстоятельством, что все частицы жидкости проходят через соответствующее живое сечение А'В' с одинаковой скоростью, равной средней скорости v (размеры живых сечений АВ и А'В' и расходы Q данных потоков считаются одинаковыми).

Обозначим через КД (М) и КЭ (М) соответственно количество движения и кинетическую энергию некоторой массы М жидкости, проходящей через живое сечение АВ за время dt (см. схему а). Через [КД (М) ]_ср и [КЭ (М)]_ср обозначим соответственно количество движения и кинетическую энергию той же массы М жидкости, проходящей через живое сечение А'В' за то же время dt (см. схему б).

Как видно, величины КД (М) и КЭ (М) должны подсчитываться в пред­положении, что скорости и в разных точках рассматриваемого живого сече­ния различны (см. схему а); величины КД (М) и КЭ (М) будем назы­вать действительными. Величины же [КД (М) 1_ср и [КЭ (М) ]_ср должны подсчитываться в предположении, что скорости и во всех точках рассматриваемого живого сечения одинаковы и равны средней скорости v см. схему б); величины [КД (М)]_ср и [КЭ (М)]_ср условно будем называть (средними» (вычисленными по средней скорости v).

Наша задача должна заключаться в количественном сопоставлении ве­личин КД или КЭ, найденных для схемы а и схемы б. Другими словами, мы должны выяснить вопрос о том, как влияет неравномерность распределения скоростей по живому сечению (см. схему а) на величины КД и КЭ массы М, найденные исходя из рассмотрения схемы б. Данный вопрос будет решен, если мы найдем величины отношений:

КД (М) : [КД (М) ]_ср и КЭ (М) : [КЭ (М)]_ср.

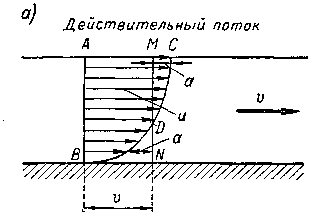
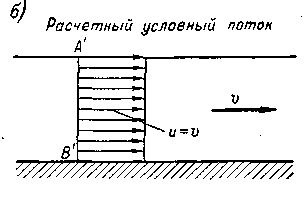
Рис. 3-24. К вопросу о коэффициентах 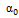и

Обращаясь крассмотрению этого вопроса, выпишем предварительно следующие соотношения, справедливость которых должна быть ясна из предыдущего изложения (см. формулы (3-29), (3-30), (3-31)):

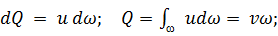(3-77)

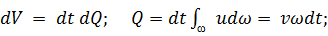(3-78)

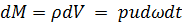; (3-79)

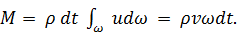(3-80)

Здесь: d 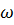— площадь элементарной площадки живого сечения; v — сред­няя скорость; V — объем жидкости, проходящей за время dt через живое сечение; М — масса этого объема.

1°. Влияние неравномерности распределения скоростей и по плоскому живому сечению на величину количества движения (КД) массы М. Дей­ствительное количество движения массы dM:

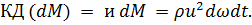(3-81)

Действительное количество движения массы М:

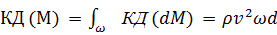(3-82)

«Среднее» количество движения массы М:

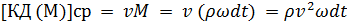. (3-83)

Существенно подчеркнуть, что

КД(М)> [КД(М)]_ср

Т. е., например, всегда имеем: (a ² + b² + с²) > d² + d² + d², где

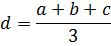
Действительно

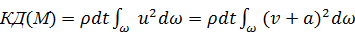(А)

где а есть положительная или отрицательная величина, переменная по живому сечению и равная а= и— v (см. рис. 3-24, а).

Из рассмотрения этого чертежа видно, что

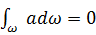(Б)

коль скоро площадь МCD должна равняться площади BDN. Имея это в виду, выражение (А) можно представить так:

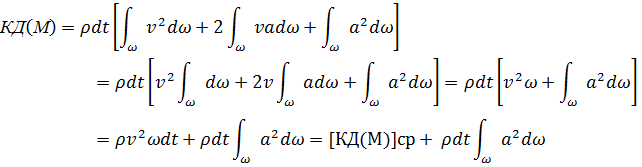
где последнее слагаемое всегда представляет собой положительную величину и обращается в нуль, только когда а = 0, т. е. когда и = v (имеем равномерное рас­пределение действительных скоростей по живому сечению); это положение и подтвер­ждает справедливость неравенства (3-84).

Разделим (3-82) на (3-83):

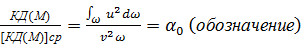(3-85)

Пользуясь введенным обозначением 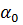можем написать

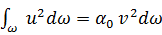(3-86)

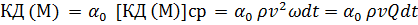(3-87)

Из (3-87) ясно, что действительная величина количества движения массы жидкости М, проходящей за время dt через рассматриваемое живое сечение, равна условной («средней») величине количества движения (подсчитанной в предположении, что все частицы жидкости проходят данное живое сече-кие с одинаковой скоростью v), умноженной на некоторый безразмерный поправочный коэффициент 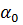. Следует запомнить, что поправочный коэф­фициент а₀ равен отношению действительного количества движения к «сред­нему» количеству движения массы М.

2°. Влияние неравномерности распределения скоростей и по плоскому живому сечению навеличину кинетической энергии (КЭ) массы М. Дей­ствительная кинетическая энергия массы dM [см. (3-79)]:

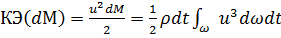(3-88)

Действительная величина кинетической энергии всей массы

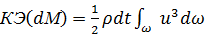(3-89)

«Средняя» (условная) кинетическая энергия массы М: «Средняя» (условная) кинетическая энергия массы М:

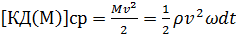(3-90)

Подчеркнем, что[14]

КЭ(М)>[КЭ(М)]_ср (3-91)

Разделим (3-89) на (3-90):

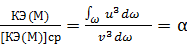(3-92)

Пользуясь введенным обозначением а, можем написать:

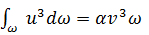(3-93)

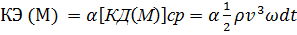(3-94)

Из (3-94) ясно, что действительная величина кинетической энергии массы жидкости М, проходящей за время dt через рассматриваемое живое сечение, равна условной («средней») кинетической энергии (подсчитанной исходя из средней скорости и), умноженной на некоторый безразмерный поправочный коэффициент а. Следует запомнить, что поправочный коэффициент а равен отношению действительной кинетической энергии к «средней» кинетической энергии массы М.

3°. Численные значения коэффициентов 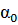и 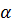. Можно показать [см., например, пояснения, относящиеся к формуле (3-84)], что а₀ и а всегда больше единицы; только при равномерном распределении скорости и по живому сечению, что в практике встречается очень редко, величины а₀ и а оказываются равными единице. Чем больше неравномерность распределения скоростей по живому сечению, тем больше величины 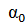и .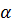

При равномерном движении жидкости (см. § 3-11, п. I^е) вели­чины а₀ и а, установленные на основании опытов, часто оказываются рав­ными:[15]

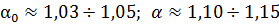
При неравномерном движении значения а„ и а могут иногда значительно отличаться от единицы. Вместе с тем очень часто в практике мы встречаем такие случаи движения жидкости, когда величины а₀ и ос все же достаточно близки к единице. Поэтому при выполнении гидравлических расчетов коэф­фициенты а₀ и а часто принимаются равными единице, т. е. при расчетах их вовсе не учитывают.

Коэффициенты ос₀ и а удобно именовать: а₀ — коррективом количества движения потока и а — коррективом кинетической энергии потока. Иногда их называют: 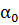— коэффициентом Буссинеска и 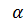— коэффициентом Корио-лиса.