При параллельноструйном и плавно изменяющемся движениях

жидкости (первое вспомогательное положение)

Рассмотрим случай установившегося движения, причем будем считать, что объемными силами, действующими на жидкость, являются только силы тяжести. Напомним, что при параллельноструйном и плавно изменяю­щемся движениях расчетные живые сечения плоские (§ 3.-8, п. 2°).

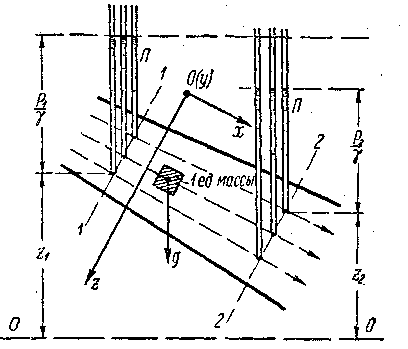
Рис. 3-23. Распределение давления в плоских живых сечениях

Представим на рис. 3-23 плав­но изменяющийся поток, причем наметим два плоских живых сече­ния 1—1 и 2—2; к различным точкам этих сечений присоединим пьезометры. Как показывает опыт, в случае указанного движения го­ризонт воды во всех пьезомет­рах, присоединенных к разным точкам одного и того же сечения (например, сечения 1—1), устанав­ливается на одном и том же уров­не. Для различных точек данного живого сечения величины z и ply имеют разное значение, однако сумма их постоянна:

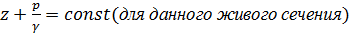(3-72)

если движение жидкости плавно изменяющееся или параллельноструйное. В другом живом сечении (например, в сечении 2—2) сумма 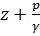будет иная, но постоянная для всех точек этого сечения. Выражение (3-72) мо­жно прочесть так: при параллельноструйном и плавно изменяющемся движе­ниях сумма отметки z и пьезометрической высоты для всех точек данного живого сечения постоянна.

Вспомним понятие потенциального напора:

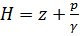(3-72)

Ранее было доказано (§ 2-8), что в случае покоящейся жидкости

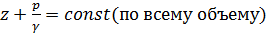(3-73)

Таков закон гидростатики. Как видно, этот закон в случае гидродинамики относится только к живым сечениям; в связи с этим часто говорят так: при параллельноструйном и плавно изменяющемся движениях жидкости распре­деление давления в данном плоском живом сечении потока следует гидростати­ческому закону. В этом и заключается первое вспомогательное положение, которое понадобится нам при переходе от элементарной струйки к целому потоку.

Данное положение можно обосновать и теоретически, пользуясь дифференциальными уравнениями движения (3-6). Располагая оси координат так, чтобы оси Оу и Оz лежали в пло­скости, параллельной живым сечениям (а ось Ох была направлена вдоль течения), можем напи­сать

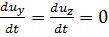(3-75)

поскольку эти выражения представляют собой составляющие ускорений, лежащих в плоскости живых сечений; величиной же таких составляющих в случае плавно изменяющегося движения мы должны пренебрегать (см. § 3-8, п. 2°).

При наличии соотношений (3-75) два последних дифференциальных уравнения Эйлера (3-6) перепишутся в виде

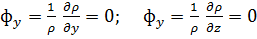(3-76)

Эти два уравнения движения ничем не отличаются от соответствующих двух дифферен­циальных уравнений равновесия жидкости (см. § 2-3). Так как именно уравнениям (3-76) подчиняется распределение давления в плоскости живых сечений, то заключаем, что в этих сече­ниях при плавно изменяющемся, а также при параллельноструйном движении, давление будет распределяться так же, как и в покоящейся жидкости.

Здесь необходимо сделать следующую оговорку. Уравнения движения (3-6) были полу­чены для идеальной жидкости. Поток же, представленный на рис. 3-23, образован реальной жидкостью, отличающейся от идеальной наличием сил трения. Однако влиянием сил трения в данном случае можно пренебречь. Поэтому уравнения (3-76) здесь оказываются справедли­выми и для реальной (вязкой) жидкости.