Энергетическая интерпретация уравнения Бернулли для элементарной струйки идеальной жидкости при установившемся движении

Рассмотрим три слагаемых, составляющих полный напор [см. (3-65)], с энергетической точки зрения. Как известно из гидростатики, первые два слагаемых представляют собой потенциальный напор:

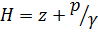(3-67)

т. е. удельную энергию потенциальную, являющуюся мерой потенциальной энергии, принадлежащей единице веса жидкости.

Третье, новое слагаемое u²/(2g) — скоростной (кинетический) напор — представляет собой удельную энергию кинетическую, т. е. меру кинетической энергии, принадлежащей единице веса жидкости. Чтобы убедиться в этом, возьмем массу жидкости М, движущуюся со ско­ростью и. Вес этой массы равен Mg, где g — ускорение силы тяжести. Энер­гия кинетическая (ЭК) массы М

(ЭК) =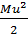

энергия кинетическая, отнесенная к единице веса массы М, т. е. удельная энергия кинетическая

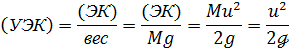
Как видно, полный напор Н'_е представляет собой сумму двух напоров: потенциального напора и скоростного (кинетического) напора h_u = u²/(2g). Можно сказать также, что полный напор представляет собой сумму трех напоров: геометрического г, напора давления ply и скоростного напора u²l(2g), причем сумма первых двух напоров равна удельной энергии потенциальной (УЭП).

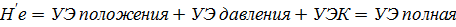
Таким образом, величину Н'_е следует рассматривать как удельную энергию полную движущейся жидкости. Согласно уравнению Бернулли, удельная полная механическая энергия, несомая жидкостью, является постоянной вдоль элементарной струйки, если жидкость идеальная. Отдель­ные энергии вдоль струйки могут изменять свою величину, но сумма их вдоль струйки идеальной жидкости должна быть неизменной. Как видно, уравнение Бернулли выражает известный закон сохранения энергии, при­мененный к случаю движения жидкости.