Уравнение Бернулли для элементарной струйки идеальной жидкости при установившемся движении

Для вывода уравнения Бернулли используем известную из механики теорему, касающуюся изменения кинетической энергии. Напомним, что эта теорема читается так: изменение кинетической энергии² рассматриваемого тела на некотором его перемещении равно сумме работ всех сил (внешних и внутренних), приложенных к данному телу, на том же перемещении.

Возьмем элементарную струйку потока (рис. 3-20). Выделим сечениями 1—1 и 2—2 некоторый отсек струйки АВ. Обозначим через z₁и z₂ превыше­ния сечений 1—1 и 2—2 над плоскостью сравнения OO, через 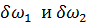— площади живых сечений струйки в сечениях 1—1и 2—2.

Будем считать, что за время 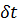отсек АВ струйки переместится в положе­ние А'В' при этом сечение 1—1 струйки переместится на расстояние 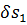и сечение 2—2 струйки — на расстояние 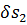. Заметим, что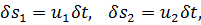

где и₁ и и₂ — скорости в сечениях 1—1и 2—2.

Рассуждая, как и в § 3-9, можем показать, что объемы элементарных отсеков струйки АА' и ВВ' равны, т. е.

объем (АА') = объему (ВВ') = 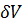(обозначение),

причем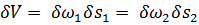

где 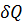— расход жидкости для струйки.

Обозначим массу элементарного объема 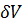через :

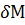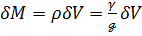(3-55)

где 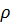— плотность жидкости.

Найдем теперь изменение кинетической энергии отсека АВ при переме­щении его в положение А'В' и работу сил, приложенных к этому отсеку, на указанном перемещении.

1°. Изменение кинетической энергии отсека АВ при перемещении его в положение А'В'. Обозначим упомянутое изменение кинетической энергии (КЭ) через б (КЭ). Тогда можно написать (см. рис. 3-20):

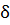(КЭ) = КЭ (А'В') — КЭ (АВ) = КЭ (А'В -f ВВ') —

— КЭ (АА' + А'В) = КЭ (ВВ') — КЭ (АА'),

т. е.

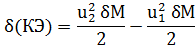
или, учитывая (3-55),

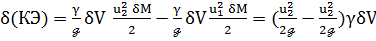( 3-56)

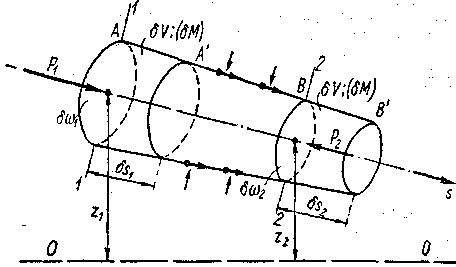
Рис. 3-20. К выводу уравнения (3-60)

2°. Работа сил при перемещении отсека АВ в поло­жение А'В'.При указанном перемещении получаем работу следующих сил.

1. Работа силы тяжести. Как видно, эффект действия силы тяжести проявился как бы в том, что отсек АА' переместился в положение ВВ' (а отсек А 'В остался на месте). Пользуясь такой условной схемой работу силы тяжести (РСТ) получаем в виде

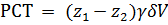(3-57)

Справедливость (3-57) может быть обоснована и более строго. Разбиваем отсек А'В на элементарные отсеки объемом 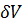. Тогда иско­мая работа силы тяжести может быть представлена в виде:

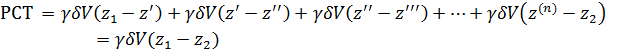
где z', z", z", . . ., z ⁽ⁿ⁾ — возвышения над плоскостью 00 граничных сече­ний, выделяющих элементарные объемы .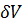

2. Работа сил гидродинамического давления,
действующего на торцовые сечения1—1 и 2—2 отсека
АВ (со стороны окружающей его жидкости). Эта работа

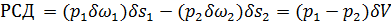(3-58)

где 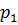и 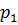— гидродинамические давления соответственно в сечениях 1—1 и 2—2.

3. Работа внешних сил давления окружающей ж ид кости на боковую поверхность отсека АВ. Эта работа равна нулю, так как силы направлены перпендикулярно к перемещениям жидких частиц, движущихся вдоль боковой поверхности отсека АВ.

4. Работа внутренних сил давления (нормальных сил взаимодействия отдельных частиц жидкости, составляющих объем АВ).

Эти силы являются парными (противоположно направленными) с одинако­выми перемещениями. Сумма работ их равна нулю.

5. Работа внешних и внутренних сил трения равна нулю (силы трения в рассматриваемой нами идеальной жидкости отсут­ствуют).

3°. Окончательный вывод. Используя теорему изменения кинетической энергии, можем написать:

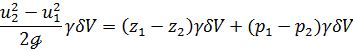
Разделим это выражение на 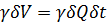, т. е. отнесем его к еди­нице в е с а того объема жидкости, который проходит за время б/ через живое сечение струйки. При этом полученное уравнение представим в виде

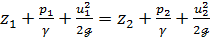(3-59)

Так как сечения 1—1 и 2—2 были намечены произвольно, то (3-59) можно переписать также в виде:

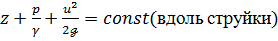(3-60)

Уравнение (3-59) или (3-60) называется уравнением Бернулли. Оно было получено Даниилом Бернулли в 1738 г. Это уравнение относится только к элементарной струйке идеальной жидкости.

Обратим внимание еще на следующее:

1) уравнение Бернулли связывает величины z, р, и;

2) как видно из (3-60), в случае идеальной жидкости сумма трех слагае мых z, , 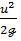является постоянной величиной вдоль рассматриваемой струйки;

3) если указанная постоянная величина для данной струйки равна A_lt то для соседней струйки сумма приведенных трех слагаемых равняется А₂, причем в' общем случае А₁ ≠ A₂;

4) зная для данной струйки постоянную величину А, а также зная для данного сечения струйки из трех величин (z, и, р) какие-либо две величины, мы можем, пользуясь уравнением Бернулли, найти третью неизвестную величину для рассматриваемого сечения струйки.

Уравнение (3-60) можно получить также путем интегрирования дифференциальных урав­нений Эйлера (см. § 3-3) для любой системы объемных сил, действующих на жид­кость и имеющих потенциал (см. § 9-2). Уравнение (3-60) относится к определенной линии тока (точнее: к элементарной струйке, намеченной вдоль определенной линии тока). Это уравнение часто называют интегралом Бернулли.

Более подробное рассмотрение данного вопроса показывает, что уравнение Бернулли (интеграл Бернулли) оказывается справедливым как для безвихревого (потенциального) уста­новившегося движения, так и для вихревого установившегося движения идеальной жидкости, при условии, однако, что на жидкость действуют объемные силы, имеющие потенциал (в част­ности, сила тяжести, которую мы имели в виду выше). При рассмотрении установившегося вихревого движения идеальной жидкости под скоростью и, входящей в уравнение Бернулли, следует понимать (так же как и в случае безвихревого движения) скорость, относящуюся к дей­ствительному векторному полю, отражающему рассматриваемое движение жидкости (к разло­жению движения на три его вида, поясненных в § 3-4, здесь обращаться не следует).

Можно также показать, что в случае: а) без вихревого (потенциального) движения идеальной жидкости и б) объемных сил, действующих на жидкость, имеющих потен­циал, величина А, о которой говорили выше, является одинаковой для всех линий тока, образующих поток: А₁= А₂= А₃ = --- В этом случае уравнение (3-60) оказывается справед­ливым для всей области, занятой жидкостью, а не только для определенной линии тока.