Уравнение неразрывности (или сплошности) движущейся жидкости в случае установившегося движения

1°. Случай резко изменяющегося движения жидкости. Представим на рис. 3-14 поток (струю) жидкости и наметим два его живых сечения 1—1 и 2—2. Рассмотрим отсек abed, заключенный между этими сечениями и ограни­ченный с боков поверхностью АВ, образованной линиями тока. Будем счи­тать, что этот

отсек принадлежит пространству и является неподвижным,жидкость же протекает через него.

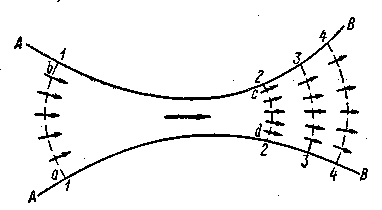
Рис. 3-14. К выводу уравнения (3-38)

Обозначим через Q₁ и Q₂ расходы соответственно для сечений 1—1 и 2—2. За время dt в отсек abcd через живое сечение 1—1поступит объем жидкости, равный Qxdt; за это же время через живое сечение 2—2 из отсека abcd выйдет объем жидкости, равный Q₁dt. Учтем следующие три обстоятель­ства:

1) проникновение жидкости через боковую поверхность АВ отсека abcd невозможно, так как эта поверхность образована линиями тока (траектория­ми) вдоль которых одна за другой движутся частицы жидкости:

2) жидкость является несжимаемой;

3) жидкость движется сплошным потоком, без образования в нем разры­вов (ограничимся рассмотрением только такого случая; вопросов кавитации, аэрации потока и т. п. [см. § 1-5] здесь касаться не будем).

Имея в виду эти три обстоятельства, можем утверждать, что объем жид­кости Q_xdt должен быть равен объему жидкости Q₂dt:

Q₁dt = Q₂dt (3-35)

или

Q₁ = Q₂ (3-36)

Помимо сечений 1—1 и 2—2, можно наметить целый ряд других живых сечений: 3—3, 4—4 и т. д. Рассматривая все эти сечения так же точно, как и сечения 1—1 и 2—2, можно прийти к выводу, что

Q₁= Q₂ = Q₃ = … = Q = const, (3-37)

т. е.

Q= const (вдоль потока). (3-38)

Как видно, если жидкость движется без образования разрывов, то при установившемся движении расход Q для всех живых сечений потока (ограни­ченного с боков линиями тока, т. е. при условии отсутствия бокового притока или оттока жидкости) одинаков.

Уравнение (3-38) и является искомым уравнением. Оно отражает свой­ства несжимаемости (см. выше п. 2) и н е р а з р ы в н о с т и, дру­гими словами, сплошности (см. выше п. 3) движущейся жидкости. Поэтому данное уравнение следовало бы называть уравнением несжимаемости и неразрывности (сплошности) движущейся жидкости. Мы, однако, будем далее именовать его просто уравнением неразрывности.

Заметим, что уравнение (3-38) можно распространить и на любые поперечные сечения потока (не обязательно только на его живые сечения); важно только, чтобы при поясненных выше условиях (см. пп. 1—3) рассматриваемые сечения полностью пересекали данный поток жидкости. При этом уравнение (3-38) можно переписать в виде: Q = const (для всех по­перечных сечений потока), где Q — объем жидкости, проходящей в единицу времени через любое поперечное сечение потока.

2°. Случай плавно изменяющегося и параллельноструйного движений жидкости. В этом случае оперируют плоскими живыми сечениями, причем величину Q выражают зависимостью (3-32). Имея это в виду, для плавно изме­няющегося и параллельноструйного движений уравнение неразрывности (3-38) можно представить еще в виде

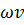= const (вдоль потока), (3-39)

откуда получаем: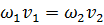

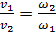(3-40)

Как видно, средние скорости обратно пропорциональны площадям живых сечений потока.

Если бы вместо целого потока жидкости мы рассматривали только эле­ментарную струйку его, то уравнения (3-39) и (3-40) для такой струйки следовало бы переписать в виде.

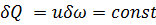(вдоль струйки); (3-41)

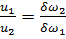(3-42)