Установившееся и неустановившееся движения жидкости.

Представим на рис. 3-6 поток жидкости, ограниченный на чертеже линиями а₁Ь₁ и а₂Ь₂. Возьмем точку 1 пространства, причем будем считать, что эта точка является неподвижной при протекании через нее жидкости. Далее наметим ряд жидких частиц М, которые, двигаясь в общем случае по разным траекториям, попадают в точку 1 в различные моменты времени t: частица М' — в момент t' частица М" — в момент t'' и т. д.

При неустановившемся движении скорость (и) в каждой данной точке пространства, например в точке 1, изменяется с течением времени, т. е. в общем случае получаем следующее:

частица М', придя в точку 1 пространства, имеет в этой точке в момент времени t’скорость u'

частица М", придя в ту же точку / пространства, в другой момент вре­мени t" имеет в этой точке другую скорость и" и т. д.

В точке 2 пространства получается аналогичная картина. Следовательно, при неустановившемся движении

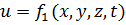(3-26)

При установившемся (или иначе, стационарном) движении каждая точка пространства характеризуется определенной, не изменяющейся во времени скоростью (и); частицы М', М", М'", . . ., придя в точку 1 в различные моменты времени, будут иметь в этой точке одну ту же скорость и (постоянную по величине направлению).

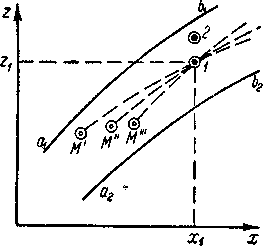
Рис. 3-6. Схема траекторий ча­стиц жидкости при неустано­вившемся движении

При установившемся движении

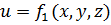(3-27)

т. е. здесь и не зависит от времени, а потому в случае установившегося движения

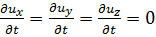(3-28)

Если бы мы учитывали сжимаемость жидкости, то к соотношениям (3-28) нам следовало бы добавить еще условие 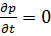, так как с изменением давления (во времени) плотность сжимаемой жидкости должна изменяться. Для абсолютно же несжимаемой жидкостиуказанное дополнительное условие является излишним.

В общем случае для установившегося движения величина .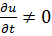

Разумеется, вместо условия (3-28) писать условие 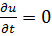нельзя, так как равенство нулю этой производной указывает лишь на то, что величина скорости не изменяется во времени; направление же скорости при этом во времени может изменяться.

При установившемся движении траектории частиц М, прохо­дящие через одну и ту же точку 1 пространства (см. линии М' — 1, М" — 1,M" — 1на рис. 3-6), характеризуются следующим:

эти траектории совпадают друг с другом (сливаются в одну линию);

они являются неизменными во времени.

Рисунок 3-6 относится к общему случаю неустановившегося движения. В случае установившегося движения получаем картину, представленную на рис. 3-7.

Справедливость сказанного можно доказать следующими рассуждениями. При установившемся движении (рис. 3-7) частица М', придя в точку про­странства 1, получает в этой точке определенную скорость и₁ и уходит из этой точки в определенном направлении (в направлении скорости ы_х), при­чем по истечении времени dt попадает в точку пространства 2, где получает скорость и₂. Следующая частица М", придя в точку 1, получит здесь ту же самую скорость и_х и уйдет из этой точки в том же самом направлении, причем по истечении времени dt окажется в точке 2, и т. д.

Рассматривая неустановившееся движение, можем разли­чать:

а) случай, когда скорость в отдельных точках пространства изменяется

относительно медленно, в связи с чем величинами 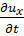, , 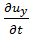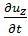можно

пренебрегать:

б) случай, когда скорость в отдельных точках пространства изменяется относительно быстро.

Первый из указанных случаев неустановившегося движения (п. «а») условимся называть медленно изменяющимся движением,[3] а второй случай (п. «б») -быстро изменяющимся движение м.