Три основных вида движения жидкости. Понятие вихревого и безвихревого движений.

Возьмем некоторое твердое тело А (рис. 3-4, а). Наметим две какие-либо частицы этого тела (частицу а и частицу Ь), причем соединим эти две частицы прямой ab. При движении данного твердого тела прямая ab будет всегда сохра­нять свою длину. Поэтому, как известно, любое движение твердого тела мо­жет быть представлено как сумма только двух движений:

поступательного, при котором упомянутая прямая ab всегда сохраняет одно и то же направление (остается при перемещении тела параллельной своему начальному направлению);

вращательного, при котором прямая ab поворачивается отно­сительно, например, точки а.

В случае движения жидкости вопрос осложняется тем, что отрезок ab, соединяющий две определенные частицы жидкости (частицу а и частицу Ь), при течении жидкости изменяет свою длину. Изменение при дви­жении жидкости длин произвольно намеченных отрезков ab обусловливает изменение формы движущихся объемов жидкости. Такое положение отсутствует в случае твердого тела. Это тело при движении все время сохраняет свою форму.

Можно показать (после соответствующего строгого обоснования), что в общем случае движение элементарного объема жидкости оказывается воз­можным представить как сумму не двух, а трех различных движений: 1) поступательного; 2) вращательного (как в случае твер­дого тела); 3) особого д в и ж е н и я, обусловливающего изменение формы движущихся объемов жидкости; этот последний вид движения назы­вается деформационным.

Рассмотрим данный вопрос подробнее. Представим на рис. 3-4, б пучок бесконечно малых лучей одинаковой длины, равной dr, исходящих из центра О. Концы радиусов dr расположатся по окружности.

Рассмотрим элементарный объем жидкости, ограниченный этой окруж­ностью. Предположим, что за время dt данный элементарный объем переме­стится в новое положение (центр его О переместится в точку O’).

Рассматривая такое элементарное перемещение выделенного жидкого объема, можем движение его разложить, как только что было отмечено, на три разных вида:

1) поступательное движение; благодаря этому движению центр О пучка радиусов перемещается в точку О'; выделяя это движение, надо в точке О' представить себе начальную окружность, ра­диусы которой параллельны соответствующим радиусам окружности с центром в точке О;

2) вращательное движение; благодаря этому движению окружность, представленная в точке О', поворачивается на некоторый средний угол dϴ; при этом поясненные выше отрезки аb должны сохранять свою длину (как в случае твердого тела);

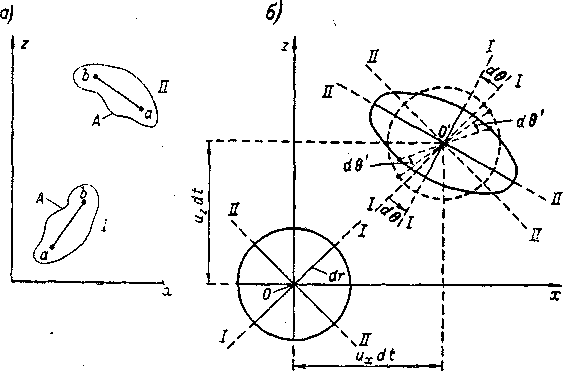
Рис. 3-4. Три вида движения жидкости

3) деформационноедвижение; благодаря этому движению каждый из намеченных радиусов поворачивается еще на дополнительны угол d ϴ'и, кроме того, удлиняется или укорачивается; величины углов dϴ' поворота (дополнительных к среднему углу, упомя­нутому в п. 2) и величины укорочения или удлинения разных радиусов будут различны; поэтому начальная окружность с центром О претерпевает дефор­мацию и обращается в фигуру, изображенную сплошной линией на чертеже. Высказанное положение о т р е х видах движения жидкости впервые было сформулировано Гельмгольцем.

Как видно, движение жидкости в общем случае можно условно предста­вить себе как движение бесконечного множества бесконечно малых волчков (частиц жидкости), которые перемещаются поступательно и при этом вра­щаются относительно своих мгновенных осей, а также еще деформируются (изменяют свою форму).

Остановимся на дополнительном пояснении второго вида движения (вращательного). Угловую скорость вращения элементарных объемов жид­кости относительно своих мгновенных осей обозначим через Ω, а компо­ненты ее — через Ω_x, Ω_y, Ω_z. Найдем соответствующие выражения для вели­чин Ω_x, Ω_y и Ω_z. С этой целью выделим элементарный объем жидкости в виде прямой треугольной призмы abc (рис. 3-5). Через аА обозначим биссектрису угла cab.

Предположим, что поступательного движения нет; имеются только вра­щение и деформация. Тогда при движении объема abc начальная точка а будет оставаться на месте. За время dt рассматриваемый объем abc:

а) в результате вращения примет положение ab'c', причем биссектриса аА повернется на угол dϴ и получит направление аА';

б) в результате деформации примет окончательную форму ab"c".

Надо считать, что в процессе деформации (п. «б») биссектриса аА должна сохранять свое направление — не поворачиваться (биссектрис! углов с'аb' и с"ab" должны совпадать). Имея в виду это положение, можем написать, что

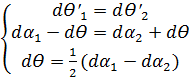(3-16)

где углы да_г и da₂ представляют собой углы поворота отрезков аb и ас (cм чертеж).

Разделив третье уравнение (3-16) на время dt, получаем:

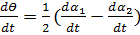(3-17)

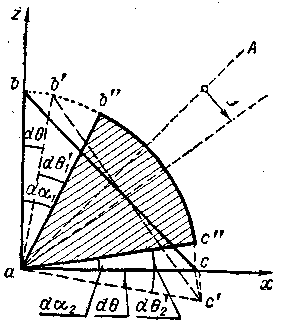
Рис. 3-5. Вращение и деформация элементарного объема жидкости

В этом уравнении величина 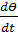представляет собой среднюю угловую скорость вращения Ω_н элементарного жидкого объем a be относительно оси у:

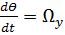(3-18)

Что касается величин, входящих в правую часть уравнения (3-17), то они равн] [см. уравнение (3-14) и пояснение к (3-15)]:

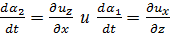(3-19)

Подставляя (3-19) и (3-18) в (3-17), получаем окончательное выражение для Ω_y; выражения для Ω_x и Ω_y пишем по аналогии:[2]

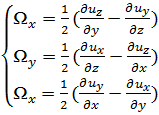(3-20)

где индексы х, у, z у величины Q указывают на то, что вращение происходи соответственно относительно осей х, у и z или вокруг осей, параллельны названным.

Геометрически складывая векторы Ω_x, Ω_y и Ω_z, можем получить векторы угловой скорости Ω, который и характеризует вращательное движение рассматриваемого элементарного объема жидкости относительно его мгновенно оси.

В частном случае, вычислив соответствующие частные производные от компонентов скорости по координатам и подставив их в (3-20), можно полу­чить величины Ω_x, Ω_y, Ω_z равными нулю. При этом обратится в нуль также и величина угловой скорости Ω. Такой частный случай будет характеризо­ваться наличием только двух видов движения: поступательного и деформа­ционного (или наличием одного из этих видов движения). В этом случае эле­ментарные объемы жидкости, перемещаясь в пространстве, не вращаются вокруг своих мгновенных осей; вернее сказать, отсутствует вращение так называемых главных осей деформации любого элементарного объема жидкости, т. е. таких трех осей этого объема, которые и после его де­формации остаются взаимно перпендикулярными. Этот частный случай движения, когда главные оси деформаций элементарных объемов движутся только поступательно, называется безвихревым дви­жением. Движение же, когда Ω ≠ 0, т. е. когда элементарные частицы вращаются относительно своих мгновенных осей, называется вихревым.