Предварительные указания
ОСНОВЫ ГИДРОДИНАМИКИ
При рассмотрении движения жидкости, вообще говоря, приходится сталкиваться с двумя различными задачами:
1) с так называемой внешней задачей; здесь задан поток жидкости, требуется же найти силы, приложенные к тому или другому твердому телу, обтекаемому жидкостью;
2) с так называемой внутренней задачей; здесь, наоборот, заданы силы, действующие на жидкость (в частности, объемные силы, например, силы тяжести); требуется же найти так называемые гидродинамические характеристики потока.
К числу гидродинамических характеристик потока относятся: а) скорость а движения жидких частиц; б) уже известная из предыдущего (см. гл.2) величина р, которая называется здесь гидродинамическим явлением.[1]
В случае идеальной жидкости гидродинамическое давление имеет тот же смысл и обладает теми же свойствами, что и гидростатическое давление р. В случае же реальной (вязкой) жидкости гидродинамическому давлению р приходится придавать особое значение.
Дело в том, что при рассмотрении элементарной призмы на рис. 2-4 в случае движения вязкой жидкости приходится учитывать касательные напряжения, возникающие по граням этой призмы (так же как и в случае твердого тела). При этом оказывается, что
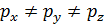
где 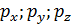 - действительные нормальные напряжения в рассматриваемой точке, относящиеся к трем произвольно намеченным в этой точке взаимно ортогональным площадкам действия.
- действительные нормальные напряжения в рассматриваемой точке, относящиеся к трем произвольно намеченным в этой точке взаимно ортогональным площадкам действия.
Имея в виду такое положение, при анализе движения вязкой жидкости пользуются гипотезой, согласно которой 
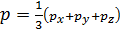
причем вычисленное таким образом значение р принимают в качестве характеристики давления напряжения) в рассматриваемой точке. Эту величину р и называют гидродинамическим давлением в точке. Как видно, в случае движения вязкой жидкости величина р не является реальным напряжением, а представляет собой среднеарифметическое значение из действительных нормальных напряжений, определенных для трех взаимно перпендикулярных площадок действия, произвольно намеченных в данной точке (считается, что величина р не изменяется с изменением ориентировки этих трех взаимно ортогональных площадок).
Ниже, главным образом, будем иметь в виду вторую (внутреннюю) задачу. При этом, как отмечено, решая ее, будем отыскивать величины и и p (зная силы, действующие на жидкость). В отношении мир надо сказать, что
в общем случае они для разных точек пространства, занятого жидкостью, имеют различную величину. Кроме того, они для данной точки пространства могут изменяться и во времени.
Учитывая сказанное, можем написать:
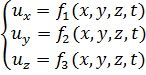 (3-1)
(3-1)
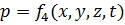 (3-2)
(3-2)
где 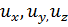 проекции скорости и на оси декартовой (прямоугольной) системы координат.
проекции скорости и на оси декартовой (прямоугольной) системы координат.
Если бы мы нашли функции 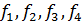 то тем самым и решили бы нашу задачу. Действительно, зная эти функции, мы могли бы для каждой точки пространства найти и и р и установить, чему для данной точки пространства равны величины и и р в различные моменты времени. Однако указанные функции очень часто отыскать нет возможности. Поэтому в гидравлике, как правило, отказываются от использования зависимостей (3-1) и (3-2) и идут по иному пути. В основу решений, приводимых в гидравлике (в технической механике жидкости), полагают другие уравнения, которые все же имеют достаточно общий характер. К числу таких основных уравнений гидравлики относятся следующие три уравнения:
то тем самым и решили бы нашу задачу. Действительно, зная эти функции, мы могли бы для каждой точки пространства найти и и р и установить, чему для данной точки пространства равны величины и и р в различные моменты времени. Однако указанные функции очень часто отыскать нет возможности. Поэтому в гидравлике, как правило, отказываются от использования зависимостей (3-1) и (3-2) и идут по иному пути. В основу решений, приводимых в гидравлике (в технической механике жидкости), полагают другие уравнения, которые все же имеют достаточно общий характер. К числу таких основных уравнений гидравлики относятся следующие три уравнения:
1) уравнение несжимаемости и неразрывности движущейся жидкости (иногда это уравнение называют уравнением баланса расхода жидкости);
2) уравнение баланса удельной энергии потока (уравнение Бернулли);
3) гидравлическое уравнение количества движения.
Эти три уравнения и составляют основную теоретическую базу технической гидродинамики. В дальнейшем в этой главе мы дадим соответствующий вывод этих уравнений (для случая так называемого установившегося движения жидкости) и подробно их разъясним. Предварительно же остановимся на пояснении некоторых, исходных представлений в основном из области кинематики жидкости.
Дата добавления: 2015-12-29; просмотров: 675;
