Потенциал скорости. Потенциальное движение жидкости
Область, занятую движущейся жидкостью, можно себе представить как векторное поле скоростей (см. рис. 2-7, а). Рассмотрим частный случай движения жидкости, когда это векторное поле является потенциальным, т. е. таким, которое может быть описано некоторой функцией 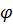 (x, у, z), обладающей следующим свойством (см. конец § 2-4):
(x, у, z), обладающей следующим свойством (см. конец § 2-4):
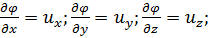 (3-21)
(3-21)
Дифференцируя первое из этих уравнений по у и второе по х, получаем:
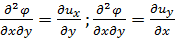 (3-22)
(3-22)
вычитая теперь из второго равенства (3-22) первое равенство (3-22), имеем:
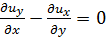 (3-23)
(3-23)
Рассуждая аналогично, можем показать, что имеют место также равенства:
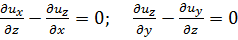 (3-24)
(3-24)
Подставляя выражения (3-23) и (3-24) в уравнения (3-20), получаем
Ωx = Ωy = Ωz = 0, (3-25)
Отсюда можно сделать следующий вывод: если рассматриваемое поле скоростей имеет потенциальную функцию (потенциал скорости 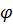 ), т. е. является потенциальным, то средние угловые скорости О. вращения частиц жидкости относительно своих мгновенных осей должны равняться нулю, и мы будем иметь безвихревое движение.
), т. е. является потенциальным, то средние угловые скорости О. вращения частиц жидкости относительно своих мгновенных осей должны равняться нулю, и мы будем иметь безвихревое движение.
Следует запомнить, что потенциальное движение всегда является безвихревым.
Можно показать, что и наоборот: безвихревое движение жидкости всегда является потенциальным.
Все существующие формы движения жидкости можно разбить на д в а вида:
а) движения безвихревые (потенциальные), обладающие потенциалом
скорости 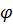 ;
;
б) движения вихревые, для которых функция 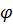 , поясненная выше, не
, поясненная выше, не
существует.
В случае потенциального (безвихревого) потока жидкости приходится отыскивать одну функцию 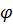 , удовлетворяющую соответствующим граничным и начальным условиям и выражающую согласно (3-21) компоненты скорости их, иу, иz.
, удовлетворяющую соответствующим граничным и начальным условиям и выражающую согласно (3-21) компоненты скорости их, иу, иz.
В случае же вихревого движения задача должна состоять, вообще говоря, в отыскании трех функций, которые должны зависеть от координат и времени, удовлетворять соответствующим граничным и начальным условиям и выражать соответственно компоненты скорости их, иу, иz.
Отсюда видно, что исследование безвихревого (потенциального) потока является задачей значительно более простой, чем исследование вихревого потока.
В случае простейших потенциальных потоков функция 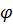 отыскивается иногда достаточно просто. Например, предположим, что нам задано движение, характеризуемое условием:
отыскивается иногда достаточно просто. Например, предположим, что нам задано движение, характеризуемое условием:
их = и0 = const; иy = 0; иz= 0.
Для такого движения траектории частиц жидкости представляют собой прямые линии, параллельные оси х, а поверхности равного потенциала ( 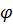 = const) — плоскости, параллельные координатной плоскости уОz. В данном случае величина
= const) — плоскости, параллельные координатной плоскости уОz. В данном случае величина
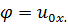
Действительно, дифференцируя это соотношение по координатам, получаем приведенные выше величины их, иу, иz.
В более сложных случаях потенциального движения для отыскания 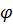 приходится пользоваться особыми методами (изучаемыми в курсах математики). Иногда может быть использован так называемый метод сложения («наложения» — суперпозиции) потенциальных потоков. Он заключается в следующем.
приходится пользоваться особыми методами (изучаемыми в курсах математики). Иногда может быть использован так называемый метод сложения («наложения» — суперпозиции) потенциальных потоков. Он заключается в следующем.
Положим, что нам известно несколько потенциальных функций: 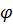 1,
1, 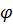 2,
2, 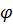 3, . . .,
3, . . ., 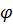 n. каждая из которых дает вполне определенный потенциальный поток.
n. каждая из которых дает вполне определенный потенциальный поток.
Возьмем алгебраическую сумму указанных функций:
 (3-25’)
(3-25’)
Можно доказать, что функция 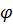 будет давать новый потенциальный поток (доказательства здесь не приводим). Такой поток будет более сложным. Например, составляющая их скорости этого потока будет
будет давать новый потенциальный поток (доказательства здесь не приводим). Такой поток будет более сложным. Например, составляющая их скорости этого потока будет
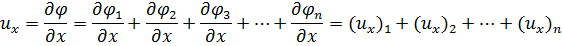
где 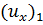 ,
, 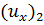 ,
,  , . . . .,
, . . . ., 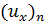 — составляющие их скорости для указанных простейших потоков, найденные в соответствующей точке.
— составляющие их скорости для указанных простейших потоков, найденные в соответствующей точке.
Из сказанного заключаем, что новый поток, описываемый функцией 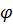 , характеризуется следующим: скорость в любой точке такого потока равна геометрической сумме соответствующих скоростей простейших потоков:
, характеризуется следующим: скорость в любой точке такого потока равна геометрической сумме соответствующих скоростей простейших потоков:
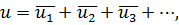
где  . — векторы скорости простейших потоков, найденные для рассматриваемой точки заданной области.
. — векторы скорости простейших потоков, найденные для рассматриваемой точки заданной области.
Если мы имеем сложный поток, то, как ясно из сказанного, для отыскания ф можно иногда поступить следующим образом. Разложить скорости и сложного потока на составляющие их (и1, и2, и3, . . ,). Рассматривая затем отдельно поле скоростей и1, и2, и3, . . , можем найти для каждого простейшего поля свою потенциальную функцию ( 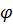 1,
1, 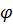 2,
2, 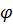 3, . . ,) Наконец, по формуле (3-25') вычислить искомую функцию
3, . . ,) Наконец, по формуле (3-25') вычислить искомую функцию 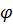 .
.
Дата добавления: 2015-12-29; просмотров: 2201;
