Основные аналитические методы исследования движения жидкости

Различают два принципиально разных аналитических метода исследова­ния движения жидкости: метод Лагранжа и метод Эйлера.

1°. Метод Лагранжа. Представим себе некоторую область, занятую движущейся жидкостью (рис. 3-1). Наметим неподвижные оси коор­динат Ох и Oz. Будем рассматривать ряд движущихся частиц жидкости: М_г, /И₂, М₃, . . ., находящихся в начальный момент времени на границе изу­чаемой области. Обозначим через х₀ и z₀ начальные координаты этих жидких частиц.

Будем считать, что для каждой частицы М нам известны зависимости

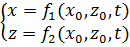(3-3)

Тогда, пользуясь этими зависимостями, легко можно построить траекто­рии намеченных частиц жидкости. Далее можем в любом месте этих траекто­рий найти длину пути ds, проходимого частицей за время dt. Деля же ds на dt, можем найти скорость в данной точке; можно так же найти и ускорение любой частицы М в любой точке пространства в тот или другой момент времени. Как видно, в данном случае мы следим за отдельными ча­стицами жидкости в течение времени t, за которое эти частицы, двигаясь по своим траекториям, проходят всю рассматриваемую область.

Согласно Лагранжу, о потоке жидкости в целом мы судим по совокуп­ному рассмотрению траекторий, описываемых жидкими частицами.

Существенно подчеркнуть, что здесь (в отличие от метода Эйлера; см. ниже) х и zпредставляют собой текущие координаты жидких ча­стиц. Поэтому величины dx и dz должны в данном случае рассматриваться как проекции пути ds на соответствующие координаты. В силу этого, со­гласно Лагранжу, можем написать:

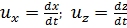(3-4)

2°. Метод Эйлера. Представим себе снова некоторую область, занятую движущейся жидкостью (рис. 3-2). Согласно Эйлеру, мы не следим за дви­жением отдельных частиц жидкости М и не интересуемся их траекториями.

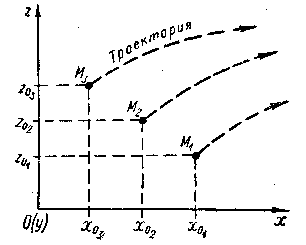
Рис. 3-1. К методу Лагранжа

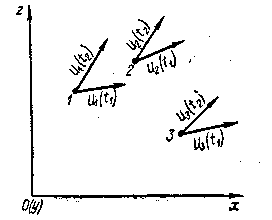
Рис. 3-2. К методу Эйлера

В соответствии с предложением Эйлера мы намечаем точки 1, 2, 3, . . ., которые считаем скрепленными с рассматриваемым пространством. Эти точки неподвижны при протекании через них жидкости. Здесь величины х и zне есть текущие координаты частиц жидкости, а просто координаты не­подвижных точек пространства.

Рассмотрим момент времени t₁. В этот момент времени в точке 1 (рис. 3-2) будет находиться некоторая частица жидкости, имеющая скорость и _t (t₁); в этот же момент времени в точке 2 будем иметь скорость и₂ ( 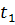) точке 3 — скорость и₃( 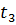) и т. д.

Как видно, для момента времени t₁ поток оказывается представленным векторным полем скоростей, причем каждый вектор скорости относится к определенной неподвижной точке пространства (и к данному моменту вре­мени t).

В следующий момент времени в точках 1, 2, 3, ... получаем соответ­ственно скорости и₁ (t₂), u₂ (t₂), и₃ (t₂),и т. д., причем в общем случае полу­чаем другое поле скоростей.

Как видно, согласно Эйлеру, поток в целом в данный момент времени оказывается представленным векторным полем скоростей, относящихся к неподвижным точкам пространства.

Сопоставляя векторное поле скоростей, отвечающее моменту времени t_lt с векторным полем скоростей, отвечающим моменту времени t_2t легко можно себе представить, как рассматриваемый поток изменяется с течением времени.

Выше было отмечено, что координаты х и z, согласно Эйлеру, являются координатами неподвижных произвольных точек пространства. Поэтому в данном случае величины dx и dz нельзя рассматривать как проекции эле­ментарного пути ds, проходимого частицами жидкости за время dt. Вели­чины dx и dz здесь являются просто произвольными приращениями коор­динат х и z. В связи с этим зависимости (3-4) в случае метода Эйлера — не­приемлемы.

3°. Метод исследования движения жидкости, применяемый в гидравлике.Метод Лагранжа ввиду его сложности не нашел широкого применения втехнической механике жидкости. Далее в основном будем пользоваться методом Эйлера. Однако, применяя его, все же не будем совершенно отрешаться от рассмотрения движения частиц жидкости М. Мы будем следить за их движе­нием, но не в продолжение времени t (как это следует по Лагранжу), а в про­должение только элементарного отрезка времени dt, в течение которого дан­ная частица жидкости проходит через рассматриваемую точку пространства. Принимая такую постановку вопроса, можем считать, что в каждой точке пространства за время dt соответствующая частица жидкости про­ходит путь ds, проекции которого равны dx и dz. При этом, очевидно, для определения проекций скорости и_х ии_г можно будет пользоваться соотноше­ниями (3-4).

§ 3-3. Дифференциальные уравнения движения идеальной (невязкой) жидкости (уравнения Эйлера)

Ранее были получены дифференциальные уравнения покоя жидкости (см. § 2-3), которые были отнесены к единице массы жидкости. Дифферен­циальные уравнения движения идеальной жидкости можно получить из указанных уравнений покоя, если согласно началу Даламбера ввести в эти уравнения силу инерции, отнесенную к единице массы движущейся жидкости. Обозначим силу инерции, действующую на единицу массы, через I; про­екции этой силы на оси координат — через I_x, I_y , I_z . При этом можем напи­сать

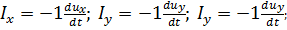(3-5)

где 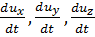проекции ускорений на соответствующие оси координат.

Сила инерции направлена в сторону, противоположную ускорению; поэтому в соотношения (3-5) входит знак минус. Вводя в уравнение (2-13)-третье слагаемое в виде (pdxdydz) I_x, представляющее собой проекцию на ось Ох сил инерции жидкого параллелепипеда (см. рис. 2-5), получаем 1-е уравнение; остальные пишем по аналогии. В результате вместо (2-14) имеем следующие дифференциальные уравнения движения идеальной жидкости (отнесенные к единице массы):

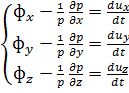(3-6)

Эти уравнения называются уравнениями Эйлера, или урав­нениями движения, или уравнениями динамического равновесия.

Надо заметить, что переходя от идеальной жидкости к реальной (вязкой) жидкости, в уравнение (3-6) приходится вводить дополнительное слагаемое, учитывающее величину сил трения, отнесенных к единице массы жидкости. Такая операция приводит нас к системе трех уравнений, называемых уравнениями Навье—Стокса (эти уравнения здесь мы не приводим)..

Учитывая (3-1), можем написать:

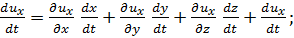(3-7)

имея же в виду (3-4), получаем следующие выражения для проекций ускоре­ния, входящих в правые части (3-6) [первое выражение вытекает из (3-7); остальные пишем по аналогии:

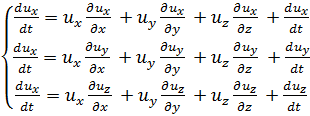(3-8)

В правые части уравнений (3-8) входит девять частных производных проекций скорости(и_х, и_у, u_z) по координатам (х, у, z). Три из этих девятипроизводных

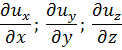
называются прямыми или продоль­ными; каждая из них взята по координате, отмеряемой вдоль той оси, на которую про­ектируется скорость. Остальные шесть частных производных называются косыми или поперечными; каждая из них берется по координате, отмеряемой поперек оси, на которую проектируется скорость.

С прямыми (продольными) производными нам придется столкнуться при выводе уравне­ния несжимаемости жидкости (см. §3-10). Здесь остановимся на пояснении физического смысла шести косых (поперечных) производных.

Физический смысл косых (поперечных) частных производных от про­екций скорости (и_х, и_у, и_z) по координатам (х, у, z). Рассмотрим для при­мера одну из шести производных, именно величину .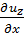

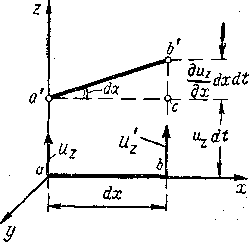
Рис. 3-3. Вращение отрезка ab

С прямыми (продольными) производными нам придется столкнуться при выводе уравне­ния несжимаемости жидкости (см. §3-10). Здесь остановимся на пояснении физического смысла шести косых (поперечных) производных.

Физический смысл косых (поперечных) частных производных от про­екций скорости (и_х, и_у, и_z) по координатам (х, у, z). Рассмотрим для при­мера одну из шести производных, именно величину .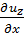

Возьмем на оси х (рис. 3-3) отрезок ab, соединяющий две частицы жидко­сти (а и 6) и имеющий бесконечно малую длину dx. Этот отрезок при движении вдоль оси 2 переместится за время dt в положение a'b', причем отрезок aa' будет представлять собой путь, пройденный в направлении оси z частицей а:

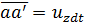(3-9)

отрезок же bb' — путь, пройденный в направлении оси z частицей b:

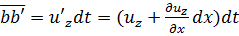(3-10)

здесь u_z — скорость движения частицы а вдоль оси z; u’_z — скорость движения частицы b вдоль той же оси z:

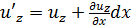(3-11)

Так как в общем случае 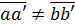то, как видно из рис. 3-3, отрезок ab за время dt совершает не только поступательное движение вдоль оси z, но еще и поворачивается относительно оси у на некоторый угол da.

Найдем угловую скорость вращения отрезка ab относительно оси у. Очевидно,

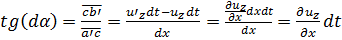(3-12)

Так как угол da мал, то тангенс этого угла можно заменить самим углом; при этом вместо (3-12) получаем:

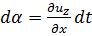(3-13)

или

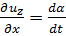(3-14)

Из этого соотношения видно, что рассматриваемая частная производная дает нам угловую скорость вращения бесконечно малого отрезка ab относительно оси у.

Исследуя точно так же остальные пять производных, легко убедиться, что все они представляют собой соответствующие угловые скорости вращения бесконечно малого отрезка ab (относительно осей х, y и z). Таков физический смысл рассматриваемых шести частных производных:

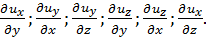(3-15)

Ясно, что первые две производные дают угловые скорости вращения в плоскости ух (относительно оси z); вторые две производные — угловые скорости в плоскости yz (относительно оси х); третьи две производные — угло­вые скорости в плоскости xz (относительно оси у).