Линия тока и элементарная струйка

1°. Линия тока. Рассмотрим случаи установившегося и неустановивше­гося движения.

1. Случай установившегося движения. Линия тока в случае установившегося движения представляет собой неизменную во вре­мени траекторию, вдоль которой одна за другой движутся частицы жидкости (см. линию М’’’ — М’’—М’—1—2; рис. 3-7).

2. Случай неустановившегося движения. Рассмо­трим некоторый момент времени 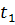. Представим себе точку 1, скрепленную с пространством (рис. 3-8). Отложив по длине вектора и₁, относящегося

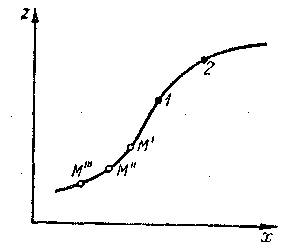
Рис. 3-7. Схема траекторий ча­стей жидкости М’ М", М''' при установившемся движении

к этой точке, небольшой отрезок 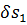, получим точку 2; далее по длине вектора скорости и₂, относящегося к точке 2, отложим небольшой отрезок 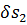; при этом получим точку 3, и т. д. В результате такого построения имеем в общем случае ломаную линию 1-2-3. . .. Подчерк­нем, что скорости u₁, и₂, u₃, ... относятся к рассматриваемому моменту времени .

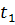Если теперь длина отрезков 6s будет стре­миться к нулю, то в пределе вместо ломаной линии 1-2-3. . . получим кривую ли­нию, проходящую через точку 1, причем эта кривая будет характеризоваться тем, что в данный момент времени 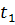во всех ее точках векторы скорости будут к ней касательны. Полученная кривая и называется л и нией тока.

Как видно, линия тока в случае неустановившегося движения есть кри­вая, проведенная внутри потока так, что в данный момент времени векторы скорости во всех точках этой кривой являются касательными к ней.

В следующий момент времени 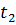скорость в точке 1 может изменить свое направление. Поэтому в общем случае неустановившегося движения линия тока, отвечающая моменту t₂, будет представлять собой уже совсем другую кривую.

Надо помнить, что в общем случае неустановившегося движения система линий тока, проведенных через начальные точки 1, 1’, 1’’, . . ., выражает только мгновенную картину движения жидкости (отвечающую опре­деленному моменту времени).

Только в том частном случае, когда с течением времени скорости и изме­няют лишь свою величину (направление же скоростей и остается постоянным), система линий тока при неустановившемся движении оказывается неизмен­ной во времени; при этом линии тока и в случае неустановившегося движения являются траекториями частиц жидкости. Разумеется, в общем случае не­установившегося движения линии тока не будут представлять собой траекто­рий жидких частиц.

2°. Элементарная струйка.Представим на рис. 3-9 поток жидкости, наметим внутри потока точку 1 и у этой точки, как показано на рисунке, выделим элементарную площадку 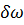, ограниченную контуром К. Далее через все точки площадки 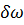проведем линии тока, отвечающие определен­ному моменту времени.

Совокупность линий тока, проведенных через все точки элементарной площадки , называется элементарной струйкой.[5] Элементарная струйка представляет собой как бы пучок линий тока. Можно сказать также, что элементарная струйка представляет собой часть движущейся жидкости, ограниченную системой линий тока, проведенных через все точки бесконечно малого простого замкнутого контура К, находящегося в области, занятой жидкостью.

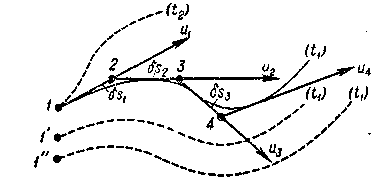
Рис. 3-8. Линии тока при неустановив­шемся движении

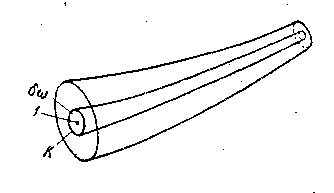
Рис. 3-9. Элементарная струйка

В случае установившегося движения элементарная струйка обладает следующими тремя свойствами.

1. Так как линии тока (рис. 3-7) при установившемся движении жидко­сти с течением времени не меняют своей формы (являются «застывшими» во времени), то и струйка тока является неизменной во времени.

2. Так как боковая поверхность струйки образована линиями тока, вдоль которых одна за другой скользят жидкие частицы, то, следовательно, проникновение жидкости через боковую поверхность невозможно. Элемен­тарная струйка как бы заключена в жесткие, не изменяющиеся во времени, водонепроницаемые стенки, не имеющие толщины.

3. Так как площадка 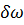является элементарной, то величины и и р для всех точек данного поперечного сечения струйки следует считать одина­ковыми. Однако вдоль струйки величины и и р в общем случае могут изме­няться.

Далее в настоящей главе условимся рассматривать в основном только установившееся движение. Вопросам неустановившегося движения посвящена глава 9.