Уравнение несжимаемости движущейся жидкости в дифференциальной форме.

Представим на рис. 3-15 оси координат х и г; ось у наметим перпендикулярно к плоскости чертежа. Возьмем некоторую неподвижную точку пространства А, определяемую координа­тами х, y, z.

Составляющие скорости и в точке А для определенного момента времени t обозначим через

u_x , u_y , u_z .

Выделим у точки А элементарный параллелепипед[9] 1—2—3—4; бесконечно малые длины его сторон обозначим через dx, dy, dz (размер dy перпендикулярен к плоскости чертежа). Дан­ный параллелепипед считаем как бы скрепленным с неподвижным пространством. Определим объем жидкости, поступившей в него за время dt, и объем жидкости, вышедшей из него (через его грани) за то же время dt.

Если в точке А горизонтальная составляющая скорости равна и_х, то в точке М_х, удален­ной от точки А на расстояние dx, горизонтальная составляющая скорости (с точностью до величин высшего порядка малости) в точке же М, горизонтальная составляющая скорости

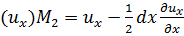(3-44)

где 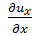представляет собой изменение величины и_х, приходящееся на единицу длины, измерен­ную вдоль линии М₁М₂, параллельной оси Ох.

Объем жидкости, вышедшей из параллелепипеда за время dt через грань 1—2,

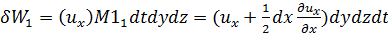(3-45)

где dy dz — площадь грани 1—2.

Объем жидкости, вошедшей в параллелепипед за время dt через противоположную грань 3—4

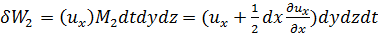(3-46)

Изменение объема жидкости в параллелепипеде за время dt за счет движения .жидкости через две противоположные его грани 1—2 и 3—4 будет

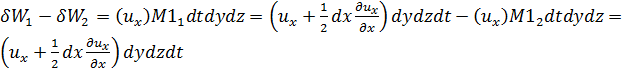(3-47)

Аналогичные выражения можно написать для остальных двух пар противоположных граней парал­лелепипеда:

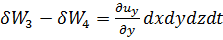(3-48)

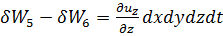(3-49)

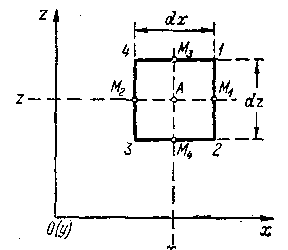
Рис. 3-15. К выводу уравнения (3-51)

где индексами 3, 4, 5, 6 указаны объемы жидкости, протекающей за время dt через соответ­ствующие грани параллелепипеда (третья и четвертая грани параллелепипеда параллельны плоскости чертежа; расход жидкости через эти грани определяется проекцией скорости и на ось у).

Считая жидкость несжимаемой, можем написать;

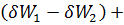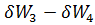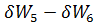( )+( ) =0 (3-50)

Подставим в эту зависимость выражения (3-47), (3-48) и (3-49); сокращая результаты на dx dy dz dt, окончательно получим

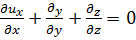(3-51)

Это уравнение и может быть названо уравнением несжимаемости однород­но й движущейся жидкости (записанным в дифференциальной форме).

Уравнение (3-51) можно было бы вывести, подсчитывая не объемы жидкости, поступившей в элементарный параллелепипед и вышедшей из него, а массы этих объемов. При этом уравне­ние (3-51) оказалось бы «отнесенным к единице массы» (так же как и уравнение Эйлера; см. § 3-3).

Частные производные, входящие в (3-51), являются продольными (прямыми) производными (см. § 3-3). Из (3-51) ясно, что сумма трех продольных частных производных, вычисленных для любой точки пространства, занятого движущейся несжимаемой жидкостью, не может являться произвольной величиной. Эта сумма (для данного момента времени) всегда должна равняться нулю.

В случае газообразных тел (являющихся сжимаемыми) сумма продольных (прямых) част­ных производных может быть не равна нулю. Однако величина этой суммы (называемая ско­ростью объемного расширения газа) и здесь должна подчиняться определенному закону.

В отличие от уравнения неразрывности (см. § 3-9), уравнение несжимаемости жидкости (3-51) относится только к точке пространства, занятого движущейся жидкостью. Поэтому уравнение (3-51), строго говоря, не отражает условий сплошности (неразрывности) движущейся жидкости: при соблюдении соотношения (3-51) разрывы жидкости конечных размеров(например, кавитационные разрывы) вблизи рассматриваемой точки могут появляться. Несмо­тря на указанное обстоятельство, уравнение (3-51) часто в литературе называют, так же как и уравнение (3-38), уравнением сплошности (или неразрывности) движения жидкости.