Сводка классификаций движений жидкости

1". Неравномерное и равномерное движения жидкости.Рассмотрим отдельно установившееся и неустановившееся движения.

1)Установившееся движение.

Представим на рис. 3-16 продольный разрез потока. Наметим несколько живых сечений его и несколько линий тока. Точки, принадлежащие одной и той же линии тока и лежащие в разных живых сечениях (см. точки 1', 2', 3', . . ., или 1", 2", 3", . . . и т. д.), могут быть названы соответствен­ными точками.

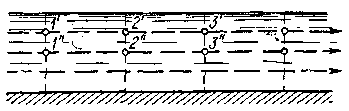
Рис. 3-16. Соответственные точки (1', 2',3',..,; 1",2",3" ...)

Рис. 3-17. Неравномерное движение

Рис. 3-18. Неравномерное дви­жение в цилиндрическом тру­бопроводе

Неравномерным движением называется такое движение, при котором:

а) или живые сечения вдоль потока изменяют свою величинуω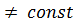
(рис. 3-17);

б) или живые сечения вдоль потока сохраняют свою величину ω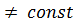

, но скорости в соответственных точках (и₁ , и₂ , и₃ …)

неравными друг другу: и₁ ≠ и₂ ≠ и₃ ≠…На рис. 3-18 представлен такой случай неравно­мерного движения. Площадь Q эпюр скоростей, показанных на рис. 3-18, разумеется, всюду одинакова (Ω₁ = Ω₂)> поскольку площадь Q выражает величину расхода. Однако форма эпюр скоростей по длине потока изменяется, причем мы и получаем так называемое нерав­номерное движение жидкости.

Равномерным движением на­зывается движение, при котором 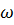= const (поток имеет цилиндрическую форму), причем скорости и в соответствен­ных точках одинаковы. При равномерном движении эпюры скоро­стей для всех сечений имеют не только одинаковую площадь, но и совер­шенно одинаковую форму.

Равномерное движение является параллельноструйным движением (эти два термина, по существу, представляют собой как бы сино­нимы)[10]. Живые сечения при равномерном движении—плоские, причем средняя скорость v при таком движении всегда

v =const (вдоль потока). (3-52)

Однако это условие является еще недостаточным для определения равномер­ного движения [в случае неравномерного движения, представленного на рис. 3-18, также удовлетворяется условие (3-52)].

Что касается неравномерного движения, то именно внутри этого вида движения следует различать:

а) движение, плавно изменяющееся (когда живые сечения считаются
плоскими);

б) движение, резко изменяющееся (когда живые сечения нельзя считать
плоскими).

2) Неустановившееся движение.

Не следует смешивать понятие равномерного (или неравномерного) движения данной частицы жидкости с понятием равномерного (или неравномерного) движения жидкости (т. е. одновременного движения множества «жидких частиц»). Кроме того необходимо учиты­вать, что при определении рассматриваемых понятий применительно к случаю неустановивше­гося движения исходят из представлений Эйлера (а не Лагранжа; см. § 3-2). В связи с этим, рассматривая векторное поле, отвечающее данному моменту времени, считают, что если это поле является рав­номерным, то ему отвечает движение, кото­рое может быть названо равномер­ным в данный момент вре­мени; если же это поле скоростей является неравномерным, то отвечающее ему движение, естественно, должно быть названо неравномерным в дан­ный момент времени.

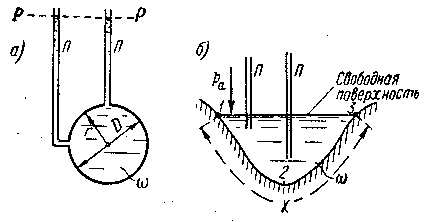
Рис. 3-19. Напорное (а) и безнапорное (б) дви­жение (х — смоченный периметр)

Из сказанного ясно, что при неуста­новившемся равномерном движе­нии жидкости (в данный момент времени) отдельные жидкие частицы движутся не­равномерно (во времени, согласно Ла-гранжу).

2°. Напорное и безнапорное движения жидкости,свободные струи.

Представим на рис. 3-19 две схемы поперечного сечения потока (а и б).

Напорным движением называется такое движение, при котором поток со всех боковых сторон ограничен твердыми стенками (рис. 3-19, а).

Безнапорным движением называется движение, характе­ризуемое наличием свободной поверхности (рис. 3-19, б).

Свободной струей жидкости называется поток (струя), вовсе не ограниченный твердыми стенками. Примером свободной струи может яв­ляться так называемая пожарная струя, выходящая из брандспойта.

3°. Гидравлические элементы живого сечения потока.Различают три основных гидравлических элемента живого сечения:

1)площадь живого сечения ;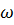

2) смоченный периметр 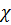, представляющий собой периметр той части поперечного сечения русла, которая смочена движущейся жидко­стью (см. линию 1—2—3 на рис. 3-19, б; для круглого сечения на рис. 3-19, а величина 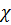=. 2 , где r — радиус сечения);

3)гидравлический радиус

(3-53)

Величина R не имеет особого физического смысла; при помощи этой ве­личины пытаются приближенно учесть влияние ф о р м ы, а также размеров живого сечения потока на движение жидкости.

Для схемы на рис. 3-19, а

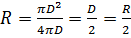(3-54)

гдеD — диаметр круглой напорной трубы.

Для круглого живого сечения гидравлический радиус равен половине геометрического радиуса.

При помощи гидравлического радиуса R в гидравлических расчетах удается учесть с неко­торым приближением форму поперечного сечения русел сравнительно «правильного» очертания (круглого, трапецеидального, приближающегося к круглому и трапецеидальному и т. п.). В случае сечений «неправильного» очертания (например, встречающегося в практике машино­строения звездообразного сечения, характеризуемого наличием острых углов) гидравлический радиус уже является непригодным для учета формы поперечного сечения русла.

4°. Сводка классификаций видов движения жидкости.На протяжении предшествующего изложения был введен ряд классификаций видов движения жидкости (по различным признакам). Все эти классификации можно предста­вить в следующем виде:

1-я классификация; здесь все возможные виды движения разби­вались на две категории:

1) безвихревое (оно же. потенциальное) движение, когда вращение эле­ментарных частиц жидкости отсутствует;

2) вихревое движение.

2-я классификация:

1) установившееся (стационарное) движение;

2) неустановившееся (нестационарное) движение: а) медленно изменяю­щееся и б) быстро изменяющееся.

Эту классификацию проводили по признаку зависимости движения жид­кости от в р е м е н и.

3-я классификация:

1) равномерное движение, оно же параллельноструйное (v = const, причем эпюра скоростей не деформируется вдоль потока);

2) неравномерное движение (v =f const или v = const, но эпюра ско­ростей деформируется вдоль потока); внутри этого вида движения различаем:

а) плавно изменяющееся движение (живые сечения принимаются плоскими);

б) резко изменяющееся движение (живые сечения криволинейны).

Здесь потоки классифицировались в зависимости от геометриче­ской формы линий тока (с учетом вопроса о деформации эпюры скоростей вдоль потока).

Впрочем, вопрос о деформации эпюры скоростей вдоль потока сводится также к вопросу о геометрической форме линий тока: если учесть, что расход между двумя заданными линиями тока постоянен по длине, то легко понять, что линии тока для потока на рис. 3-18 не являются параллельными прямыми (участки эпюр скоростей в сечениях 1—1 и 2—2, лежащие между двумя рассматриваемыми линиями тока, должны иметь одинаковые площади, поскольку эти площади выражают расход).

4-я классификация:

1) напорное движение (рис. 3-19, а);

2) безнапорное движение (рис. 3-19, б);

3) свободные струи.

В дальнейшем нам придется столкнуться еще со следующими двумя классификациями.

5-я классификация (см. § 3-23):

1) ламинарный режим движения жидкости;

2) турбулентный режим движения жидкости. 6-я классификация (см. § 7-6):

6-я классификация (см. § 7-6)

1) спокойное движение жидкости;

2) бурное движение жидкости.

Пользуясь приведенными шестью классификациями, можно достаточно точно определять тот или другой изучаемый вид движения жидкости.

Заметим, что следует различать еще 7-ю классификацию движений (в зависимо­сти от характера, например, векторных полей скорости и ускорения):

Все виды движения жидкости, рассматриваемой как сплошная среда (континуум), являются пространственными (носят пространственный характер). Вместе с тем внутри пространственного движения можно различать, например, следующие частные случаи его (которые и составляют упомянутую седьмую классификацию):

1) плоскопараллельное движение (сокращенно говорят «плоское движение»); это движение должно одновременно удовлетворять двум условиям: а) в данный момент времени область движения можно пересечь такими плоскими параллельными поверхностями, в которых лежат векторы скоростей и ускорений, отвечающие всем точкам этих поверхностей; б) во всех точках любого перпендикуляра, проведенного к указанным поверхностям, скорости и ускоре­ния в данный момент времени одинаковы (по величине и направлению);

2)осесимметричное движение (точнее плоскоосесимме-тричное движение); в этом случае в данный момент времени поле скоростей и ускоре­ний имеет одинаковый вид для всех плоскостей, проходящих через одну и ту же прямую, являющуюся осью симметрии данного поля скоростей (векторы скоростей и ускорений здесь, разумеется, должны лежать в упомянутых выше плоскостях);

3) линейное движение — также частный случай пространственного (и иногда пло­ского) движения — когда гидромеханические параметры жидкости (скорость, давление) могут быть представлены для данного момента времени зависящими только от одной координаты про­странства, отмеряемой обычно по известной нам оси потока (прямолинейной или криволиней­ной), вдоль которой изменяется состояние потока (т. е. скорость и давление); в направлениях, нормальных к этой оси, состояние потока считается неизменным.

Надо заметить, что иногда в указанных выше случаях вместо слова «движение» говорят «задача»: «плоская задача», «осесимметричная задача», «линейная задача», а также «простран­ственная задача».[11]