Вероятное описание потока отказов

Число отказов v_t возникающих на интервале (0 - t) как случайная величина, зависящая от параметра t, представляет случайный процесс с дискретными значениями. Реализацию такого случайного процесса представляют неубывающие ступенчатые функции от непрерывного аргумента с целочисленными значениями.

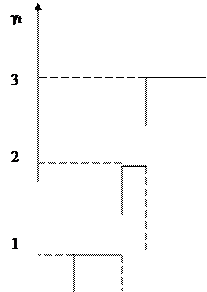Рис. 2.8. Реализация случайного процесса с дискретными значениями

Скачки, равные единице, появляются в моменты возникновения отказов. Общее вероятностное описание случайного процесса дается многомерной функцией распределения значений процесса в произвольно выбранной последовательности моментов времени.

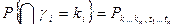(34)

где k_i…k_n – заданная неубывающая последовательность целых чисел при условии, что i_i > i_j, i > j.

В теории надежности чаще всего используется одномерная и двумерная функция распределения потока отказов:

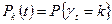(35)

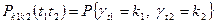(36)

Поток отказов принадлежит классу стационарных потоков, если вероятность возникновения фиксированного числа отказов на данном интервале времени зависит только от длины интервала, но не от оси времени расположения интервала. Аналитическое условие принадлежности к классу стационарных потоков можно записать

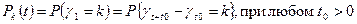(37)

т.е. вероятность возникновения фиксированного числа отказов на заданном интервале времени не зависит от выбора начала отсчета времени.

Для нестационарных потоков отказов:

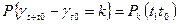(38)

Поток отказов принадлежит классу потоков без последствий, если вероятность возникновения фиксированного числа отказов на интервале (t₁,t₁ + t) не зависит от того, сколько отказов возникло до момента t₁. Аналитически условие можно записать:

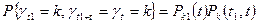(39)

Для потоков с последствиями:

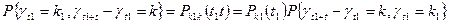(40)

Рассмотрим экспоненциальное распределение времени безотказной работы как следствие стационарности и отсутствия последствия потока отказов.

Вероятность того, что на интервале [0,(t+τ)] не возникло ни одного отказа, на основании условия стационарности и отсутствия последствий следует:

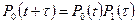
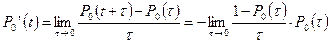
так как [1 – P₀(τ)] представляет вероятность отказов на интервале [t, (t+τ)], то 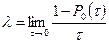представляет интенсивность отказов, постоянную для любого момента времени.

Найдем дифференциальное уравнение первого порядка, которому удовлетворяет вероятность безотказной работы P₀(t) на интервале t, если стацонарный поток без последствий:

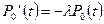
Если учесть начальные условия P₀(0) = 1, тогда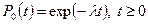

Таким образом, экспоненциальный закон распределения длительности безотказной работы следует из общего предположения о стационарности потока и об отсутствии в нем последствия.

Глава 3. Статические методы обработки данных полученных при испытаниях на надежность.

Расчетные оценки не позволяют получить ответ на главный вопрос: какова надежность изготовленной аппаратуры? Ответ можно получить непосредственно из сферы эксплуатации или испытаниями на надежность. Испытаниям на надежность подвергается выборка объема п в течение времени t. Целью разработки методов испытаний, по результатам которых можно с заданной точностью и достоверностью судить о показателях надежности.