Экспоненциальное распределение. Вероятность безотказной работы:

Вероятность безотказной работы:

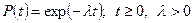(31)

Является частным случаем распределения Вейбулла при δ = 1.

При этом при δ = 1 из (30) следует, что 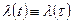, т.е. 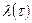- постоянная. Следовательно, экспоненциальный закон (31) определяется одним параметром λ, т.е. постоянной интенсивностью отказов. Таким образом, период нормальной эксплуатации характеризуется экспоненциальным распределением интервала безотказной работы.

Среднее время безотказной работы:

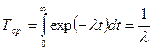(32)

т.е. равно величине, обратной интенсивности отказов.

Заменяя в (31) λ на 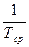, получим:

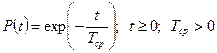(33)

Таким образом, зная среднее время безотказной работы Т_ср или постоянную интенсивности отказов 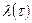, можно найти вероятность безотказной работы для интервала времени от момента включения до любого заданного момента времени t.

Вероятность безотказной работы на интервале времени равном среднему времени безотказной работы Т_ср, равна:

Длительность периода нормальной эксплуатации до наступления сарения может оказаться меньше Т_ср, т.е. интервал времени, на котором допустимо пользоваться экспоненциальной моделью, часто бывает меньше времени безотказной работы.

Дисперсия времени безотказной работы для экспоненциального распределения равна:

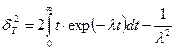
или

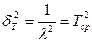
Условная вероятность того, что устройство проработает безотказно на интервале времени t, следующем за интервалом τ после включения, на котором устройство уже проработало без отказа

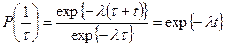
Таким образом, если устройство проработало без отказов до момента τ, то дальнейшее распределение времени безотказной работы будет таким же, как и в момент первого включения. Это свойство полностью характеризует экспоненциальное распределение и означает, что на интервале времени нормальной эксплуатации устройство не стареет.

Экспоненциальное распределение является идеальной моделью, которая отражает процесс появления внезапных отказов. Эту модель часто используют для априорного анализа, так как она позволяет несложными расчетами получить соотношения для сравнения различных вариантов построения систем.