Ортогонализация и декорреляция входных векторов
Мы выяснили, что нормирование и приведение к единой шкале увеличивают информативность данных. Однако этого оказывается недостаточно. Известно [3], что если факторы статистически зависимы, то их совместная энтропия меньше суммы энтропий отдельных факторов.
При достижении статистической независимости входов будет достигнута максимальная информационная насыщенность каждого из входных факторов в отдельности. Для достижения статистической независимости входов нейронной сети используется линейное преобразование, которое осуществляет декорреляцию входных векторов [3, 23]. Алгоритм декорреляции называется ещё "выбеливание входов" (whitening).
Рассмотрим вычислительную сущность метода. Доказательства можно найти в литературе по многомерному статистическому анализу, например, в [21, 24]. Пусть входные векторы 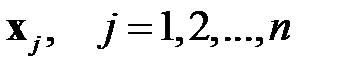 представлены в виде матрицы
представлены в виде матрицы 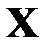 (табл. 3.2).
(табл. 3.2).
Таблица 3.2. Входные векторы
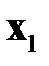
| 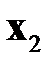
| 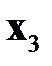
| … | 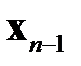
| 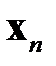
|
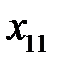
| 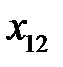
| 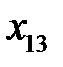
| … | 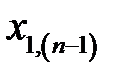
| 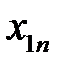
|
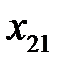
| 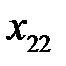
| 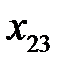
| … | 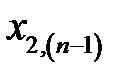
| 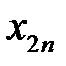
|
| … | … | … | … | … | … |
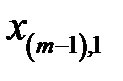
| 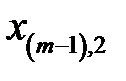
| 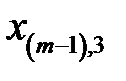
| … | 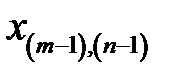
| 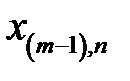
|
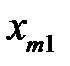
| 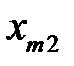
| 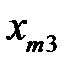
| … | 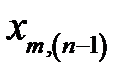
| 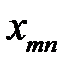
|
Тогда 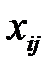 означает
означает 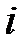 ‑й компонент вектора
‑й компонент вектора 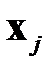 . Входные векторы будем рассматривать как случайные коррелированные векторы. Преобразуем входные векторы в центрированные, то есть в векторы с нулевым математическим ожиданием. Для этого вычислим матрицу
. Входные векторы будем рассматривать как случайные коррелированные векторы. Преобразуем входные векторы в центрированные, то есть в векторы с нулевым математическим ожиданием. Для этого вычислим матрицу 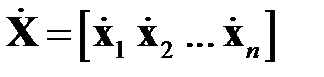 , где
, где 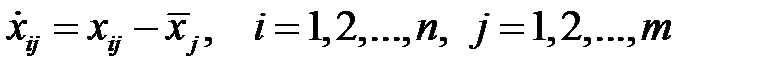 , то есть вычитаем из элементов каждого столбца его среднее значение
, то есть вычитаем из элементов каждого столбца его среднее значение
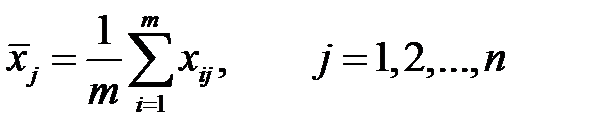 .
.
Вычислим ковариационную матрицу. Ковариационная матрица 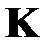 — это квадратная матрица размера
— это квадратная матрица размера 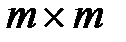 , образованная из попарных ковариаций
, образованная из попарных ковариаций 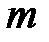 компонентов каждого вектора. Элементы ковариационной матрицы равны (используем несмещенную оценку)
компонентов каждого вектора. Элементы ковариационной матрицы равны (используем несмещенную оценку)
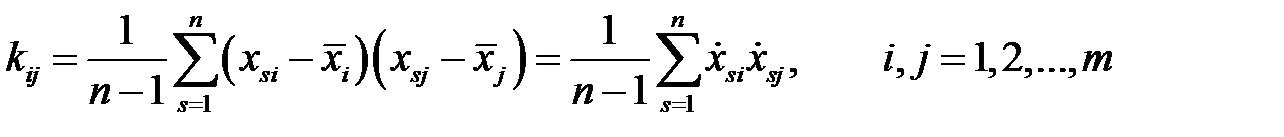 ,
,
где 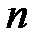 — количество входных векторов,
— количество входных векторов, 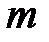 — число компонентов векторов.
— число компонентов векторов.
Ковариационную матрицу удобно рассматривать, используя скалярные произведения центрированных входных векторов
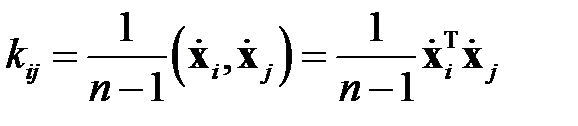 ,
,
где 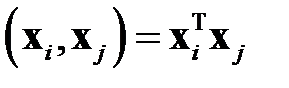 — скалярное произведение векторов.
— скалярное произведение векторов.
Тогда ковариационная матрица запишется в виде
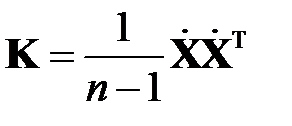 ,
,
где 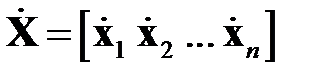 — матрица центрированных векторов.
— матрица центрированных векторов.
Матрица 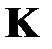 является симметричной и положительно определенной матрицей размером
является симметричной и положительно определенной матрицей размером 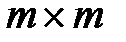 .
.
Матрица 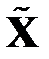 , составленная из преобразованных некоррелированных векторов, получается из исходной матрицы
, составленная из преобразованных некоррелированных векторов, получается из исходной матрицы 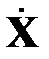 линейным преобразованием [21]
линейным преобразованием [21]
 ,
,
где 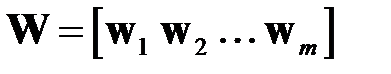 ,
, 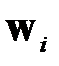 ,
, 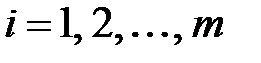 — собственные векторы матрицы
— собственные векторы матрицы 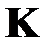 .
.
Задача на собственные значения для матрицы 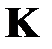 имеет вид
имеет вид
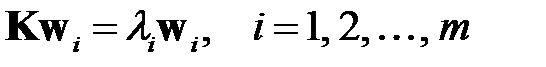 ,
,
где 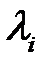 и
и 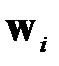 — собственные числа и соответствующие собственные векторы матрицы
— собственные числа и соответствующие собственные векторы матрицы 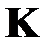 .
.
В результате преобразования столбцы матрицы 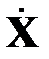 преобразуются в некоррелированные столбцы матрицы
преобразуются в некоррелированные столбцы матрицы 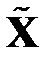 . Матрица ковариации для
. Матрица ковариации для 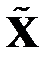 представляет собой диагональную матрицу, с диагональю из дисперсий столбцов матрицы
представляет собой диагональную матрицу, с диагональю из дисперсий столбцов матрицы 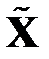 . Известно [21], что эти дисперсии равны соответствующим собственным числам матрицы
. Известно [21], что эти дисперсии равны соответствующим собственным числам матрицы 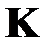 . Зачастую [3, 23] векторы исходных данных преобразуют в некоррелированные векторы с единичной дисперсией по формуле
. Зачастую [3, 23] векторы исходных данных преобразуют в некоррелированные векторы с единичной дисперсией по формуле
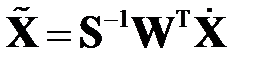 ,
,
где 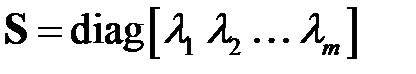 .
.
Полученные векторы будут не только некоррелированными, но и ортогональными. Действительно, два случайных вектора 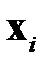 и
и 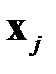 называют некоррелированными, если
называют некоррелированными, если 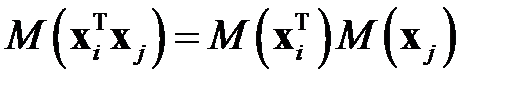 и ортогональными, если
и ортогональными, если 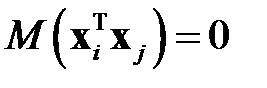 (здесь
(здесь 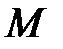 обозначает вычисление математического ожидания) [25]. В нашем случае центрированных векторов, у которых математическое ожидание равно нулю, некоррелированность векторов означает их ортогональность.
обозначает вычисление математического ожидания) [25]. В нашем случае центрированных векторов, у которых математическое ожидание равно нулю, некоррелированность векторов означает их ортогональность.
В результате ортогонализации совместная энтропия входных векторов увеличивается, поскольку распределение элементов в обучающем множестве выравнивается и становится ближе к равномерному. Но поскольку преобразованные входные векторы представлены в другой системе координат, то теряется привычный физический смысл их компонентов.
Декорреляция связана с сингулярным разложением [20] ковариационной матрицы. Учитывая симметрию матрицы 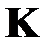 , получаем
, получаем
 ,
,
где 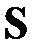 — диагональная матрица, на диагонали которой расположены собственные значения
— диагональная матрица, на диагонали которой расположены собственные значения 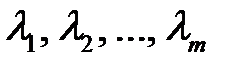 матрицы
матрицы 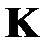 ;
;  — ортогональная матрица, столбцы которой являются собственными векторами матрицы
— ортогональная матрица, столбцы которой являются собственными векторами матрицы 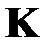 .
.
Ортогональность матрицы  означает ортогональность ее столбцов и равенство обратной матрицы транспонированной:
означает ортогональность ее столбцов и равенство обратной матрицы транспонированной: 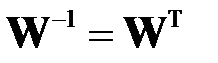 . Ортогональность столбцов означает, что они образуют базис.
. Ортогональность столбцов означает, что они образуют базис.
Матрица 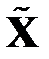 , составленная из преобразованных некоррелированных векторов, и исходная матрица
, составленная из преобразованных некоррелированных векторов, и исходная матрица 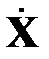 связаны соотношением
связаны соотношением
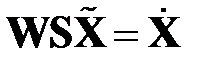 ,
,
откуда
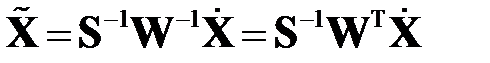 .
.
В учтено свойство ортогональной матрицы 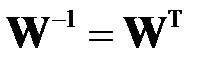 . Так как матрица
. Так как матрица 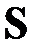 диагональная, обратная матрица легко вычисляется. Выражения и совпадают.
диагональная, обратная матрица легко вычисляется. Выражения и совпадают.
Следует отметить, что выбеливание входов не всегда дает существенный эффект, поэтому требует экспериментальной проверки.
Дата добавления: 2015-12-08; просмотров: 2318;
