Использование метода главных компонент

Популярным и мощным средством понижения размерности входных данных является метод (анализ) главных компонент (МГК), или по-английски PCA — Principal-Component Analysis. В теории сигналов такое преобразование векторов известно как преобразование Карунена‑Лоэва (Karhunen‑Loève Transformation). Это метод использует проектирование данных с высокой размерностью в пространство с меньшей размерностью [21, 24]. Метод главных компонент использует линейное преобразование, аналогичное преобразованию , использовавшемуся для ортогонализации входных векторов. Но в отличие от преобразования , в котором матрица 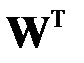имеет размерность 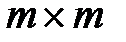, в МГК используется матрица размерностью 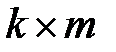, где . 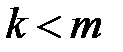В результате такого преобразования размерность преобразованных векторов будет меньше размерности исходных векторов. Преобразование МГК производится таким образом, что преобразованные векторы сохраняют наиболее важную информацию об исходных векторах. МГК применим к нормально распределенным коррелированным входным данным. Метод является одной из форм компрессии с потерей информации и преобразует большое количество взаимно коррелированной входной информации во множество статистически независимых векторов. Причем наименее изменчивая информация отбрасывается. Для построения матрицы преобразования МГК упорядочим положительные собственные значения ковариационной матрицы в порядке убывания : 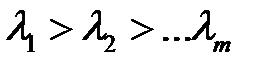(собственные значения матрицы 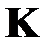являются вещественными и положительными). В аналогичной последовательности расположим соответствующие собственные векторы 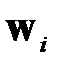. Если ограничиться 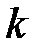максимальными собственными значениями, то матрица преобразования получит вид 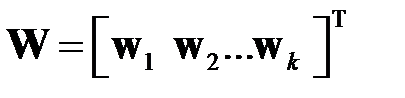. Далее производится преобразование . Относительный вклад преобразованного вектора 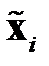в общую дисперсию равен [21]

.

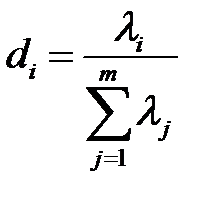В МГК отбрасываются компоненты, имеющие малое значение .

Таким образом, МГК преобразует входные векторы в ортогональные и оставляет только наиболее изменчивые векторы. Метод главных компонент производит сжатие данных. Но как уже указывалось, преобразованные векторы не несут физического смысла.

Реконструкция исходного вектора с учетом ортогональности матрицы производится по формуле

,

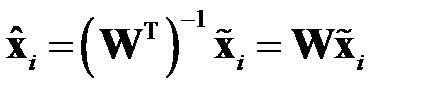где вектор 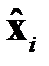близок к .

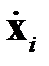Рассмотренный метод главных компонент показывает, что в случае коррелированных входных векторов пропуски компонентов векторов можно восстановить с помощью МГК (см. раздел 3.2.3).

Рассмотрим пример применения МГК, заимствованный из [32]. Вектор измерений 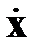представляет собой длину 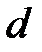, ширину 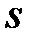и высоту 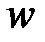различных черепах. Были произведены измерения этих параметров для популяции размером 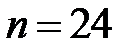. В [32] приведена ковариационная матрица

.

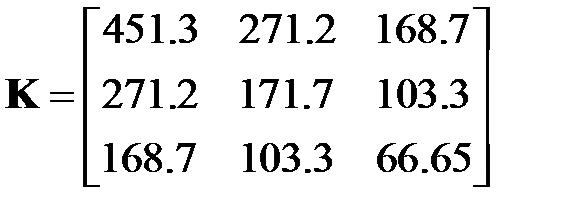В системе MATLAB получены собственные значения 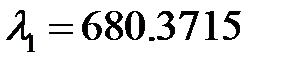, , 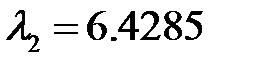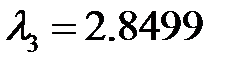и соответствующие собственные векторы[2]

.

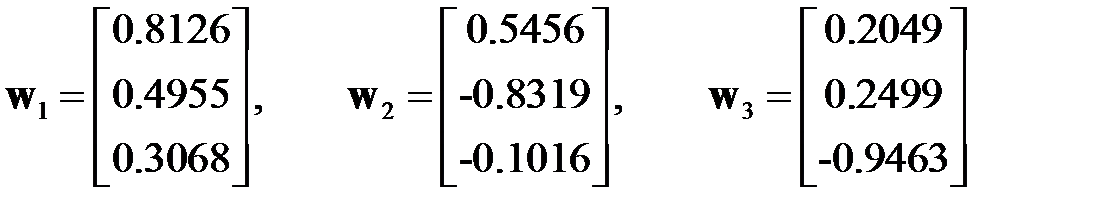Матрица преобразования имеет вид

.

Вклады главных компонентов, вычисленные по , составляют 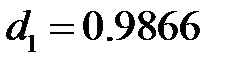, 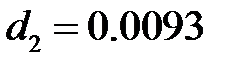и 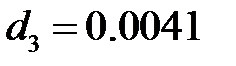. Поэтому можно ограничиться первым главным компонентом 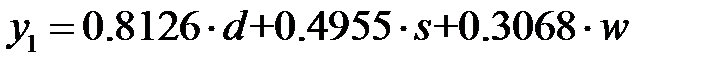. То есть каждая черепаха может быть описана не трехкомпонентным, а однокомпонентным вектором. Правда, новые векторы не несут физического смысла.

Вычисление главных компонент представляет существенную вычислительную сложность. Известны нейронные сети (сети PCA) [32, 33], вычисляющие главные компоненты.