Восстановление пропущенных компонентов данных

Во многих случаях обучающие выборки содержат пропуски (отсутствие) данных. Например, в медицине и социальных науках данные часто содержат пропуски. Известны различные методы обработки пропущенных компонентов данных [5, 11–16]. Рассмотрим обучающую выборку для обучения сети с учителем. Выборка представляет собой множество входных векторов, являющихся значениями входных факторов (признаков). Для каждого входного вектора известно значение выходного вектора (целевое значение выходного вектора). В процессе обучения на вход сети подаются входные векторы и вычисляются векторы выхода сети. Вычисляется ошибка выходных векторов по сравнению с целевыми выходными векторами. Ошибка используется для настройки весов сети по различным алгоритмам.

Восстановление пропущенных данных в обучающей выборке нейронной сети является известной задачей восстановления пропущенных данных в таблице [5]. Пусть 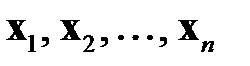— векторы входных факторов, 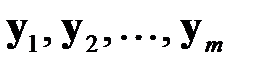— векторы выходных факторов. Тогда обучающая выборка из 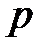примеров может быть представлена в виде таблицы 3.1. При таком представлении 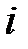‑й обучающий пример представляет собой вектор 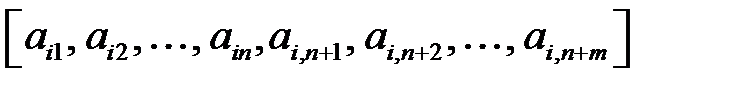. 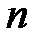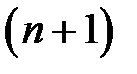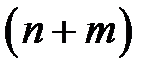Первые компонентов вектора представляют собой значения входных факторов, компоненты с по являются компонентами соответствующих целевых значений выходов сети. Будем считать, что некоторые значения в табл. 3.1 пропущены (не заполнены).

Рассмотрим некоторые методы обработки пропущенных данных.

Метод исключения некомплектных объектов.Это означает, что строки таблицы вида 3.1 с пропущенными значениями исключаются. Подход легко реализуется и может быть удовлетворительным при малом числе пропусков. Однако неполные данные могут нести в себе информацию, необходимую для исследования. Следствием такого подхода является снижение репрезентативности обучающего и тестового множеств. Даже в тех случаях, когда процент элементов выборки с пропущенной информацией относительно низок, при их равномерном распределении велика вероятность удаления из выборки важных данных и исключений.

Таблица 3.1. Структура обучающей выборки

Номер обучающего примера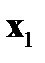

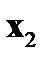
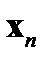
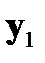
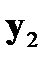
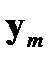
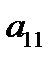
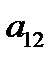
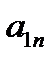
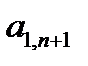
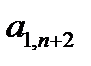
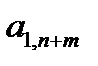
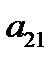
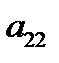
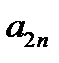
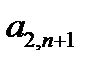
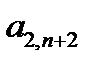
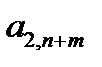
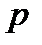
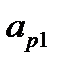
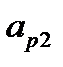
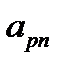
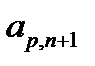
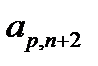
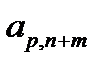
Методы с заполнением (в англоязычной литературе часто называют Imputation — вменение, приписывание [17–18]). При данном подходе пропущенные значения исходной выборки заполняются и полученные "полные" данные обрабатываются обычными методами. Эта группа методик, называемая иногда Hot Deck (англ. — "горячая колода", термин пошел со времен использования перфокарт), содержит большое количество приемов: выбор случайного значения в столбце табл. 3.1, замена отсутствующего значения его средним значением по столбцу либо величиной, предсказанной посредством регрессионного анализа, либо найденной путем поиска "ближайшего соседа", когда недостающие величины заменяются их значениями для какой-то другой строки, наиболее похожей по совокупности прочих характеристик. Наиболее часто используются следующие процедуры заполнения пропусков.

Заполнение средними значениями. Если входные данные представить в виде табл. 3.1, то пропуск в элементе 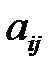заполняется по формуле

,

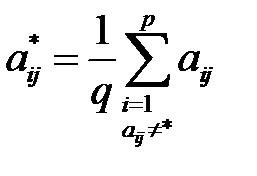где 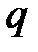— количество заполненных элементов в ‑м столбце, отсутствующие значения обозначены звездочкой.

Данный подход применим, если все значения в столбце однородны. Если в одном столбце несколько пропусков, то все они будут заполнены одинаковыми значениями.

В методе подстановки с подбором внутри групп формируются группы близких значений, и пропуски в каждой группе заполняются с помощью присутствующих значений из этой группы. Например, пропущенные значения анализов пациентов заменяются средними значениями для больных и здоровых людей. Этот подход является упрощенным вариантом рассматриваемого ниже кластерного подхода.

Неплохие результаты дает замена пропущенного значения случайным числом, распределенным по закону распределения соответствующего признака (по закону распределения значений столбца таблицы). Причем можно использовать эмпирический закон распределения.

Подбор ближайшего соседа основан на предположении, что пропущенное значение близко к заполненным значениям строк, близких к строке, содержащей пропуск. Для простоты предположим, что в таблице отсутствует единственный элемент 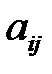. Рассматривая строки таблицы как векторы, в качестве меры близости между строками таблицы возьмем евклидово расстояние между элементами 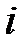‑ой и всех остальных строк таблицы. 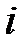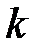Тогда расстояние между ‑ой и ‑ой ( 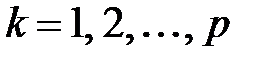) строками определится формулой

.

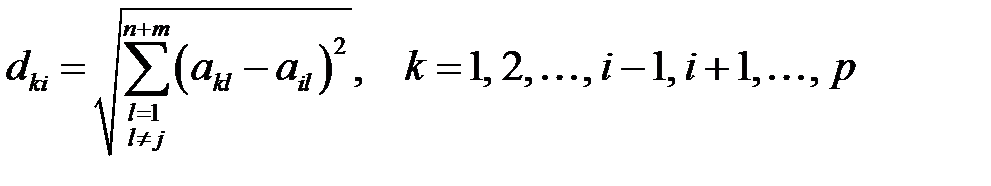Среди 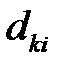выбирается 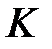минимальных значений ( 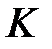назначается), тем самым определяются 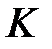ближайших соседей 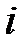‑ой строки. Обозначим множество номеров строк, ближайших к строке 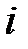, через 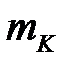. Для получения 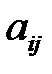элементы ‑го столбца ближайших соседей усредняются с весами, обратно пропорциональными их евклидову расстоянию до строки, содержащей пропуск

,

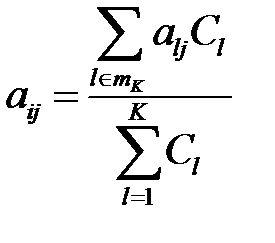где 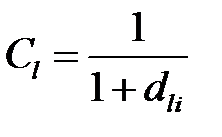— вес ‑ой строки.

Заполнение с помощью прогноза. В этом случае исходные данные разделяются на две группы: первая группа содержит все характеристики, вторая группа содержит данные с пропусками. Пропущенные значения прогнозируются с использованием данных первой группы. По своей сути заполнение с помощью прогноза использует моделирование [5], то есть строится модель зависимости отсутствующего фактора от комплектных данных. Применяются различные методы прогнозирования: линейная регрессия, аппроксимация полиномами, нейросетевые методы. Регрессионное моделирование пропусков осуществляется в два этапа.На первом этапе по совокупности комплектных данных строится регрессионная модель, и оцениваются коэффициенты в регрессионном уравнении, где в качестве зависимой переменной выступает пропущенное значение, которое необходимо восстановить. Затем по полученному на предыдущем этапе уравнению, в которое подставляются известные значения независимых переменных, рассчитывается отсутствующее значение. Нейросетевые методы подразумевают построение и обучение нейронной сети, позволяющей по полным данным предсказывать значения отсутствующих данных. Однако если отсутствующие данные можно получить с помощью прогноза, то ценность этих данных с точки зрения анализа минимальна. Скорее всего, эти данные являются избыточными.

Хорошие результаты дает кластерный метод заполнения пропусков [19]. Идея подхода заключается в группировке векторов выборки по некоторым признакам и замене пропусков данных локально в каждой группе. Пропущенные данные заменяются средними значениями в данном кластере или случайными значениями по эмпирическому распределению интересующего параметра в кластере.

Метод Бартлетта (Bartlett M. S.) [5, 11] разработан для заполнения пропусков в выходных переменных. В случае активного эксперимента значения факторов задаются исследователем, и пропуски в выходных переменных наблюдаются чаще, чем во входных факторах. В методе Бартлетта пропуску присваивается какое-то начальное значение (например, ноль или среднее арифметическое столбца), затем строят уравнение многомерной линейной регрессии с использованием начального значения пропуска, и после анализа этого уравнения предсказывается пропущенное значение.

Напомним, что линейная регрессионная модель для произвольного выходного вектора выходных факторов 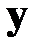табл. 3.1 (номер вектора опустим, чтобы не загромождать формулы) имеет вид

,

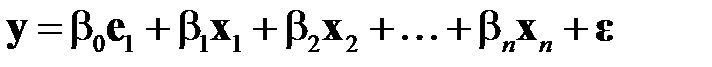где 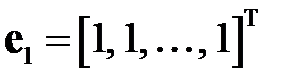— вектор‑столбец, состоящий из одних единиц; 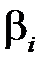— коэффициенты, определяемые методом наименьших квадратов (МНК), 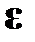— вектор остатков, характеризующий погрешность линейного представления.

В матричной форме имеет вид

,

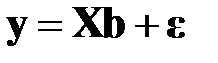где , , , .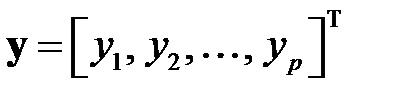

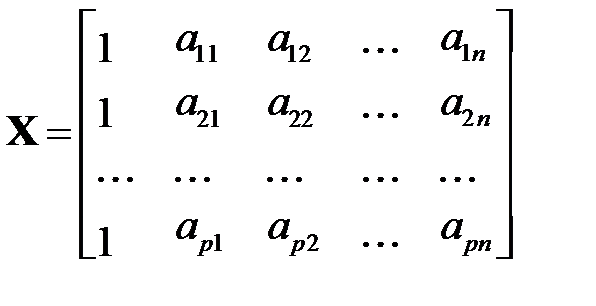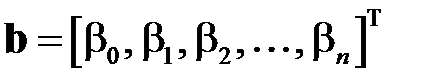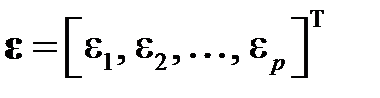При использовании МНК и пренебрежении остатками оценка вектора 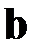формально запишется в виде

.

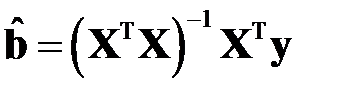Фактически обратные матрицы не находятся, а решается система линейных алгебраических уравнений. Исходя из теории МНК, нахождение вектора 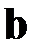представляет собой минимизация целевой функции

,

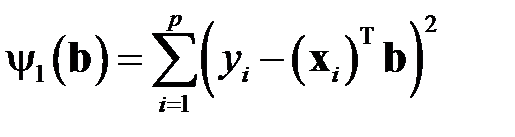где 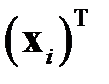— 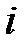‑я строка таблицы данных.

Вычислительные аспекты МНК можно найти в литературе по вычислительной математике, например, в [20]. Если матрица 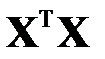не вырождена, то 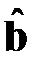является несмещенной оценкой 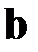с минимальной дисперсией.

Предположим, что у вектора 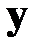пропущено 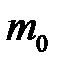первых компонентов (строки табл. 3.1 можно переставить, чтобы выполнялось это требование). Каждый пропуск 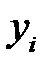, , 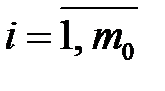заполним начальными значениями 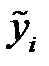. В [11] показано, что замену лучше произвести средним значением заполненных элементов столбца.

Построим матрицу размером 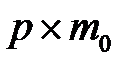сопутствующих значений переменных пропусков. По определению [11] 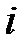-я сопутствующая переменная пропусков равна 1, если она соответствует пропущенному значению. Для присутствующих значений сопутствующая переменная равно 0. У матрицы левая верхняя подматрица размером 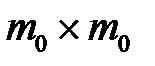представляет собой единичную матрицу (содержащую единицы только на диагонали), все остальные элементы матрицы нулевые:

.

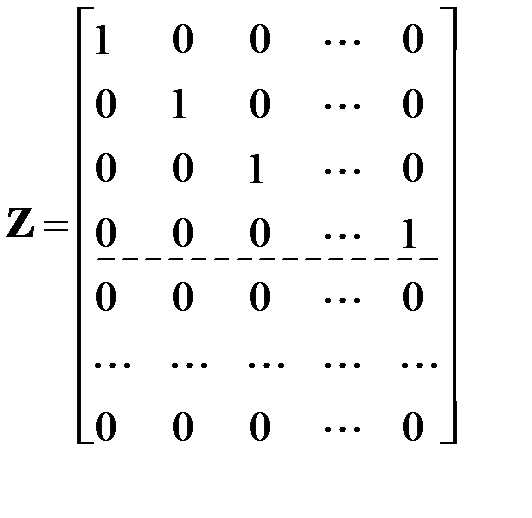Предположим, что для вектора 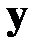верна линейная модель

,

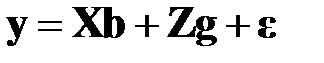где 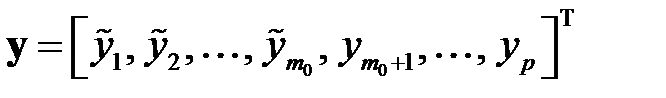—вектор выходных факторов, первые 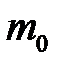элементов которого представляют собой начальные значения; 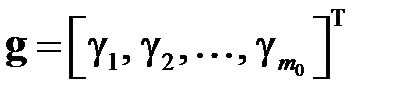— вектор‑столбец коэффициентов регрессии; остальные элементы с учетом структуры матрицы могут быть произвольными; остальные переменные — как в и .

Целевая функция задачи имеет вид

,

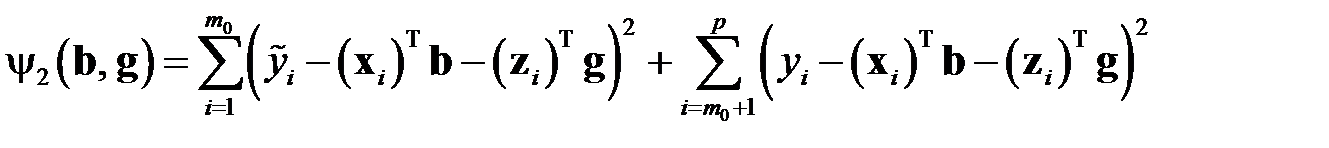где 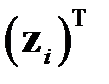— строки матрицы (примем унифицированное обозначение для строк матриц 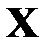и ).

Необходимо найти 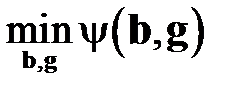. Используя определение матрицы , получим из

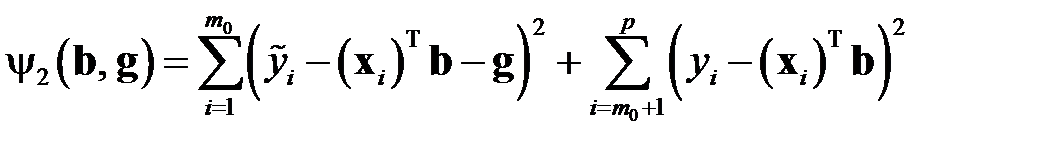
Допустим, что 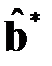— оценка, полученная методом наименьших квадратов по формуле для существующих значений 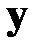, то есть по последним 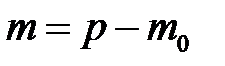строкам. Эта оценка минимизирует вторую сумму в выражении . Если при 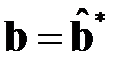положить 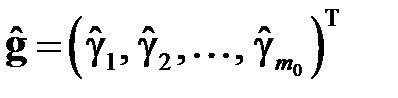, где

, ,

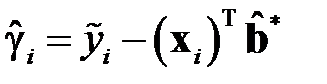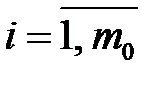то превращается в нуль первая сумма в и целевая функция принимает минимальное значение

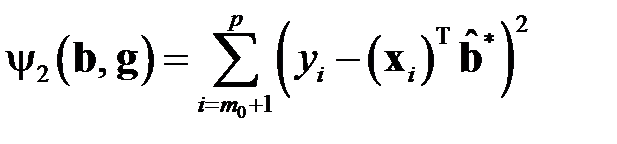
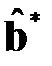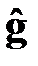Таким образом, векторы и минимизируют целевую функцию и являются оценками МНК, полученными для модели . Уравнение означает, что точная оценка МНК отсутствующего значения 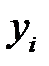, то есть 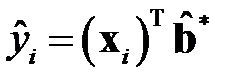, равна 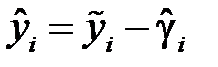. Другими словами: прогноз 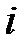-го пропущенного значения методом наименьших квадратов равен начальному значению для 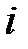‑го пропуска минус регрессионный коэффициент для сопутствующей переменной 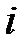-го пропуска.

Кроме рассмотренных известно множество других методов заполнения пропусков. Так алгоритм ZET [8] относится к локальным алгоритмам и в отличие от рассмотренных алгоритмов не работает со всей таблицей данных. В основе алгоритма ZET лежат три предположения. Первое состоит в том, что реальные таблицы имеют избыточность, проявляющуюся в наличии похожих между собой объектов (строк) и зависящих друг от друга свойств (столбцов). Второе предположение состоит в утверждении, что для предсказания пропущенного элемента 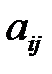нужно использовать не всю таблицу, а лишь ее "компетентную" часть, состоящую из элементов строк, похожих на строку 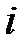, и элементов столбцов, похожих на столбец . Остальные строки и столбцы для данного элемента неинформативны. Третье предположение заключается в том, что из всех возможных видов зависимостей между столбцами (строками) в алгоритме ZET используются только линейные зависимости. В работе алгоритма ZET можно выделить три этапа.

1. На первом этапе для данного пробела из исходной матрицы "объект-свойство", столбцы которой нормированы по дисперсии, выбирается подмножество компетентных строк и затем для этих строк — компетентных столбцов.

2. На втором этапе автоматически подбираются параметры в формуле, используемой для предсказания пропущенного элемента, при которых ожидаемая ошибка предсказания достигает минимума.

3. На третьем этапе выполняется непосредственно прогнозирование элемента по этой формуле.

В простейшей модификации алгоритма Resampling [12] строки, содержащие пропущенные данные, заменяют случайно подобранными строками из матрицы полных наблюдений. Затем строится регрессионное уравнение для предсказания отсутствующего значения. Процедура построения регрессионного моделирования повторяется несколько раз. После определенного количества повторений значения полученных регрессионных коэффициентов усредняют и получают окончательное решение.

Для восстановления пропущенных данных можно использовать сингулярное разложение матриц [21]. Рассмотрим таблицу 3.1 как матрицу 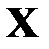размерностью 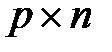. Тогда можно записать сингулярное разложение (2.24)

,

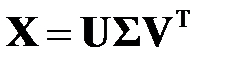где 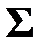— матрица вида 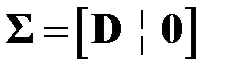, , 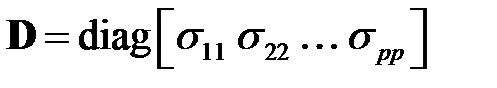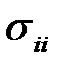— сингулярные числа, равные неотрицательным квадратным корням из собственных чисел матрицы 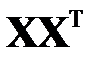, , 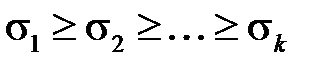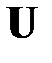и 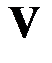– ортогональные матрицы.

Поэлементное представление выражения имеет вид

.

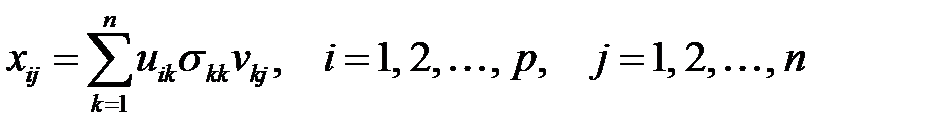Известно [21], что основные статистические характеристики матрицы 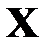определяются меньшим числом входных векторов, чем 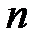. То есть в суммирование можно провести по числу слагаемых .

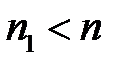Пусть в матрице 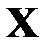пропущено значение 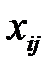. Тогда для восстановления значения 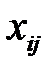по полностью комплектным векторам, число которых равно 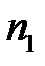, вычисляем элементы 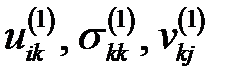и восстанавливаем значение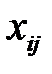

.

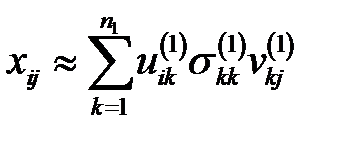Мы рассмотрели только идею применения сингулярного разложения для заполнения пропусков в данных. Детали можно найти в [21].