Виды и принципы предварительной обработки

При конструировании и использовании нейронных сетей важную роль играет предварительная обработка данных. Образно охарактеризовал ситуацию с предварительной обработкой Т. Кохонен, создатель класса нейронных сетей, названных его именем: "Нельзя пренебрегать предобработкой. Нейросетевые алгоритмы — это не машина для производства сосисок, где с одного конца подается сырье (данные), а с другого получаются результаты. Для каждой задачи необходим тщательный выбор вектора признаков, а этот этап до сих пор большей частью выполняется вручную"[1]. При рассмотрении предварительной обработки информации учтем рекомендации по предварительной (препроцессорной) обработке информации для нейронных сетей [1–5] и более общие рекомендации для аналитических систем [6–7]. Можно выделить следующие операции предварительной обработки информации.

1. Формирование обучающей выборки. Необходимо определить количество обучающих данных и оценить их качество. Определение количества обучающих данных представляет сложную проблему, связанную с размерностью данных и сложностью сети. Чем выше размерность данных, тем больше данных нужно для обучения сети. Но слишком большой объем обучающей выборки может привести к переобучению сети — потери обобщающей способности. Поэтому объем выборки определяется экспериментально с учетом сложности сети. Необходимо также провести проверку качества обучающей выборки. Для этого, прежде всего, проводятся статистические проверки на гладкость распределения обучающих данных. Необходимо также провести проверку входных данных на соответствие нормальному закону распределения, так многие статистические методы и приемы применимы только для нормально распределенных данных. Если данные распределены не по нормальному закону, то следует применять непараметрические методы, которые позволяют исследовать данные без каких-либо допущений о характере распределения переменных, в том числе при нарушении требования нормальности распределения. "Нормальность" распределения необходимо учитывать при заполнении пропусков данных и в алгоритмах обработки. Например, если данные распределены не по нормальному закону, то, строго говоря, пропуски нельзя заполнять средним значением. Пропуски следует заполнять с учетом вероятностью распределения данных.

2. Обработка аномалий, противоречий и дубликатов в данных. Обучающие данные могут содержать ошибки, выбросы, дубликаты, снижающие качество данных. Их необходимо удалить. Причем эти отклонения не всегда очевидны. Необходим тщательный анализ, что является аномалией, а что — возможным значением, важным для анализа.

3. Восстановление пропущенных данных. Некоторые данные в обучающей выборке могут быть пропущены. Зачастую исключить данные с пропусками нельзя, так как можно потерять важную информацию. Тогда необходимо заполнить пропуски правдоподобными значениями.

4. Трансформация данных, то есть представление данных в виде, удобном для обработки. Это, прежде всего, кодирование данных — то есть представление всех данных в виде чисел, и шкалирование (масштабирование) — приведение к определенному диапазону.

5. Понижение размерности исходных данных. Чем выше размерность входных данных (входных векторов), тем сложнее должна быть сеть, то есть сеть должна содержать больше весов. Чем сложнее сеть, тем труднее ее обучить. Уменьшение размерности входов сети позволяет использовать меньше данных, обеспечивая приемлемый уровень сложности сети.

Общим принципом для многих шагов препроцессорной обработки является принцип максимизации энтропии [3, 5]. Задача нейросетевого моделирования — найти статистически достоверные зависимости между входными и выходными переменными. Единственным источником информации для нейронной сети являются примеры из обучающей выборки. Чем больше информации принесет каждый пример, тем лучше используются имеющиеся в нашем распоряжения данные.

Пусть нам дана дискретная случайная величина, которая может принимать 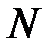значений с вероятностями 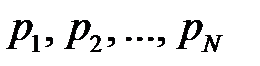. Тогда величина

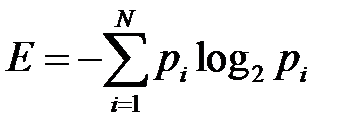
называется энтропией данной случайной величины (энтропия измеряется в битах). Содержательный смысл энтропии такой. Если мы, например, храним в памяти 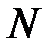значений этой случайной величины (при этом 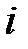-ое значение встречается с вероятностью 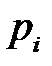), то каким бы совершенным ни был наш код, мы все равно потратим в среднем не меньше 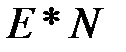бит.

Чем больше энтропия, тем меньше вероятность того, что случайная величина постоянно принимает некое определенное значение. Если значения некоторой переменной равномерно распределены в некотором интервале, то энтропия этой величины максимальна.

Простейшей моделью входных данных нейронной сети можно считать их интерпретацию в качестве отсчетов некоторой случайной величины. Таким образом, чем больше энтропия входных данных, тем больший объем информации мы имеем на входе сети и тем лучше будет обучаться сеть.