Первого порядка
Частной производной по переменной х функции 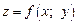 в точке
в точке 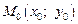 называется предел
называется предел
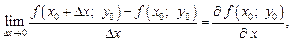 (18.1)
(18.1)
если он существует.
Производную (18.1) обозначают также 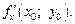
Частной производной по переменной у функции 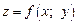 в точке
в точке 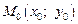 называется предел
называется предел
 (18.2)
(18.2)
если он существует.
Производную (18.2) обозначают также 
Если частные производные определены на множестве 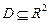 и
и 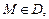 то они являются функциями двух переменных
то они являются функциями двух переменных 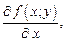
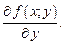
Для функции трех переменных 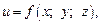 в случае их существования, аналогично определяют три частные производные
в случае их существования, аналогично определяют три частные производные 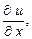
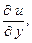
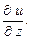
Полным приращениемфункции 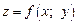 в точке
в точке 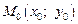 называется разность
называется разность
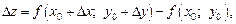
где 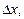
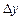 – приращения аргументов.
– приращения аргументов.
Функция 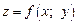 называется дифференцируемой в точке
называется дифференцируемой в точке 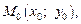 если полное приращение функции в этой точке можно представить в виде
если полное приращение функции в этой точке можно представить в виде
 (18.3)
(18.3)
где А, В – некоторые числа; 
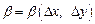 – бесконечно малые при
– бесконечно малые при 
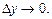
Если функция дифференцируема в точке М0, то в формуле (18.3)

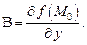
Главная часть полного приращения (формула (18.3)) дифференцируемой функции 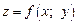 называется дифференциаломэтой функции и обозначается dz:
называется дифференциаломэтой функции и обозначается dz:
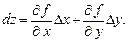 (18.4)
(18.4)
Для независимых переменных х и у дифференциалы совпадают с их приращениями: 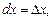
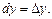
Дифференциал функции двух переменных 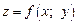 вычисляется по формуле
вычисляется по формуле
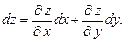 (18.5)
(18.5)
Дифференциал функции трех переменных 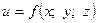 вычисляется по формуле
вычисляется по формуле
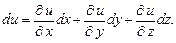 (18.6)
(18.6)
При достаточно малых 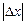 и
и 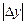 для функции
для функции 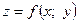 , дифференцируемой в точке
, дифференцируемой в точке 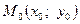 и ее окрестности, имеет место приближенное равенство
и ее окрестности, имеет место приближенное равенство
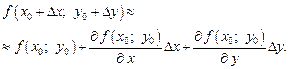 (18.7)
(18.7)
Для функции трех переменных (в случае дифференцируемости в точке М0 и малых приращениях независимых переменных) справедливо:
 (18.8)
(18.8)
Пример 1. Вычислить 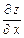 и
и  функции
функции
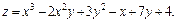 Найти значения частных производных в точке (–1, 1).
Найти значения частных производных в точке (–1, 1).
Решение. Зафиксируем у, вычислим производную по х, пользуясь правилами дифференцирования (условно считаем y = const):
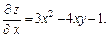
Тогда
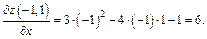
Зафиксируем х, вычислим производную по у:

Тогда
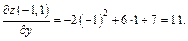
Пример 2.Найти частные производные функции
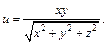
Решение.Фиксируя у и z, вычислим производную по х:
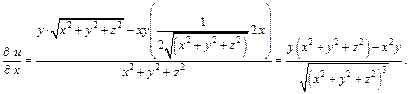
Зафиксируем x и z и аналогично вычислим производную по y:
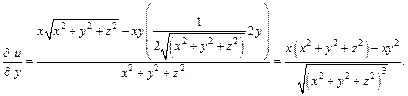
Зафиксируем x и y и вычислим производную по z:

Пример 3.Найти dz функции 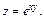
Решение. Используя формулу (18.5), найдем частные производные:

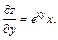
Тогда
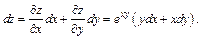
Пример 4.Найти 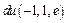 функции
функции 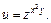
Решение.Используя формулу (18.6), вычислим частные производные:
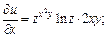
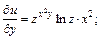
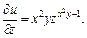
Тогда
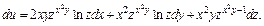
Подставим 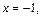
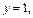
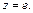
Получим:
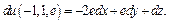
Пример 5. Вычислить приближенно 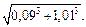
Решение.Используем формулу (18.7). Рассмотрим функцию 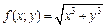 и найдем ее значение при
и найдем ее значение при 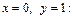

Вычислим значения частных производных функции f в точке (0; 1).
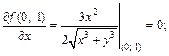

Приращения аргументов 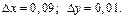
Тогда по формуле (18.7) имеем:
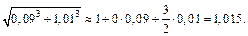
Пример 6. Вычислить приближенно 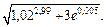
Решение.Рассмотрим функцию 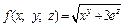 и найдем ее значение при
и найдем ее значение при 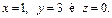 Имеем:
Имеем: 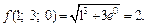
Вычислим значения частных производных в точке (1; 3; 0):
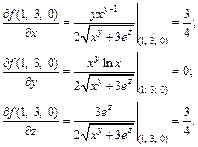
Приращение аргументов 
Используя далее формулу (18.8), получаем:
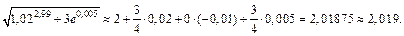
Дата добавления: 2015-09-29; просмотров: 690;
