Касательная плоскость и нормаль к поверхности
Пусть поверхность задана уравнением
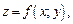
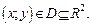
Тогда уравнение касательной плоскости в точке 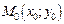 имеет вид:
имеет вид:
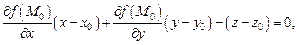 (18.16)
(18.16)
где 
Нормалью к поверхности в точке 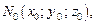
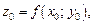 называется прямая, проходящая через точку
называется прямая, проходящая через точку 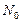 перпендикулярно к касательной плоскости в этой точке.
перпендикулярно к касательной плоскости в этой точке.
Уравнение нормали к поверхности (18.16) в точке 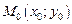 имеет вид:
имеет вид:
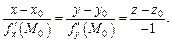 (18.17)
(18.17)
Если поверхность задана уравнением
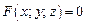 (18.18)
(18.18)
и в точке 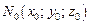 этой поверхности существуют частные производные
этой поверхности существуют частные производные 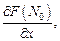
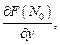
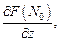 не равные нулю одновременно, то уравнение касательной плоскости к поверхности (18.18) в точке
не равные нулю одновременно, то уравнение касательной плоскости к поверхности (18.18) в точке 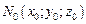 имеет вид:
имеет вид:
 (18.19)
(18.19)
Уравнение нормали к поверхности (18.18) в точке 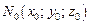 имеет вид:
имеет вид:
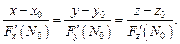 (18.20)
(18.20)
Пример 1. Поверхность задана уравнением 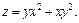 Составить уравнение касательной плоскости и уравнение нормали к поверхности в точке
Составить уравнение касательной плоскости и уравнение нормали к поверхности в точке 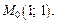
Решение.Найдем частные производные:
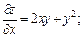
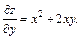
Их значения в точке 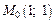 равны
равны 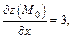
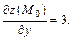
Найдем соответствующее значение 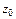 функции для
функции для 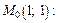
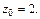
Тогда уравнение касательной плоскости примет вид:
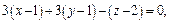
или
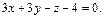
Уравнение нормали:
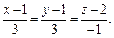
Пример 2. Составить уравнение касательной плоскости и нормали к поверхности 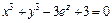 в точке
в точке 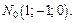
Решение.Частные производные имеют вид:
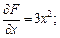
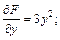
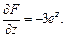
Их значения в точке N0 равны:
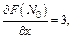
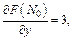
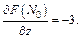
Тогда уравнение касательной плоскости в точке N0: 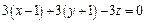 или
или 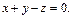
Уравнение нормали: 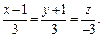
Пример 3.Составить уравнения касательных плоскостей к поверхности 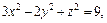 параллельных плоскости
параллельных плоскости 
Решение. Найдем частные производные:
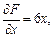
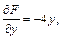
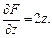
Так как касательная плоскость параллельна плоскости 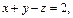 то справедливо условие параллельности плоскостей:
то справедливо условие параллельности плоскостей:
 т. е.
т. е. 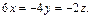
Координаты точек касания найдем из системы уравнений

Решая систему, получаем: 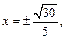
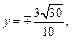
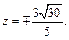
Точки касания имеют координаты:
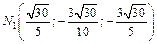 и
и 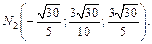
Тогда уравнения касательных плоскостей имеют вид:
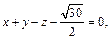
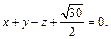
Пример 4. Составить уравнение касательной плоскости к поверхности, заданной уравнением 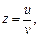 где
где 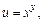
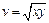 в точке
в точке 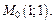
Решение.Поверхность задана сложной функцией. Найдем частные производные, используя формулы (18.11) (см. § 18.3):
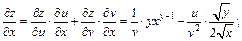

Их значения в точке 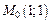 соответственно равны:
соответственно равны:
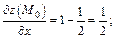
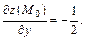
Найдем соответствующее значение 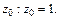
Тогда уравнение касательной плоскости:
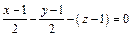 или
или 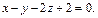
Пример 5. Записать уравнение нормали к поверхности, заданной уравнением 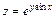 в точке
в точке 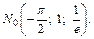
Решение.Найдем частные производные и вычислим их в точке N0:
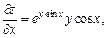
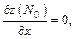
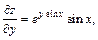
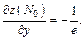
Уравнение нормали в точке N0:
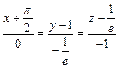 или
или 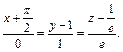
Равенство нулю 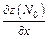 означает, что касательная плоскость параллельна оси Ох, а нормаль к ней лежит в плоскости
означает, что касательная плоскость параллельна оси Ох, а нормаль к ней лежит в плоскости 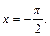
Дата добавления: 2015-09-29; просмотров: 1950;
