Экстремумы функций двух переменных
Функция 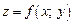 имеет в точке
имеет в точке 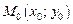 локальный максимум (минимум), если существует такая d-окрестность точки М0, что для всех точек
локальный максимум (минимум), если существует такая d-окрестность точки М0, что для всех точек 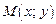 из этой окрестности (отличных от М0) выполняется неравенство
из этой окрестности (отличных от М0) выполняется неравенство
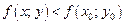

Максимум и минимум функции называются ее экстремумами (локальными), а точка М0, в которой достигается экстремум, называется точкой экстремума.
Необходимое условие экстремума: если в точке 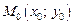 дифференцируемая функция
дифференцируемая функция 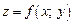 имеет экстремум, то ее частные производные в этой точке равны нулю:
имеет экстремум, то ее частные производные в этой точке равны нулю:
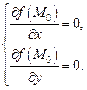 (18.34)
(18.34)
Точки, в которых частные производные существуют и равны нулю, называются стационарными.
Точки из области определения функции, в которых частные производные равны нулю или не существуют, называются критическими точками.
Не всякая критическая точка является точкой экстремума.
Достаточное условие экстремума. Пусть 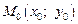 – стационарная точка дважды непрерывно дифференцируемой функции
– стационарная точка дважды непрерывно дифференцируемой функции 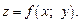 Обозначим:
Обозначим:
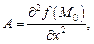
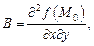
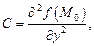
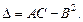
Тогда:
1) если 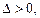 то функция имеет в точке М0 локальный экстремум (максимум при
то функция имеет в точке М0 локальный экстремум (максимум при 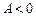 и минимум при
и минимум при 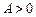 );
);
2) если 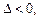 то в точке М0 функция не имеет экстремума;
то в точке М0 функция не имеет экстремума;
3) если  то в точке М0 функция может иметь локальный экстремум, а может и не иметь его (нужны дополнительные исследования).
то в точке М0 функция может иметь локальный экстремум, а может и не иметь его (нужны дополнительные исследования).
Допустим, что функция f(x; y) определена на некотором множестве 
Число С называют наибольшим значением функции (глобальный максимум) на множестве D, если
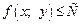
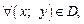 записывают так:
записывают так:
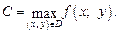
Число с называют наименьшим значением функции (глобальным минимумом) на множестве D, если
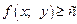
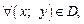 записывают так:
записывают так:
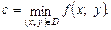
Теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множестве 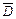 функция
функция 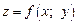 достигает на этом множестве своего наибольшего и наименьшего значений.
достигает на этом множестве своего наибольшего и наименьшего значений.
Для нахождения наибольшего и наименьшего значений функции в области 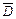 нужно:
нужно:
1) найти критические точки функции, принадлежащие D, и вычислить значение функции в них;
2) найти наибольшее и наименьшее значения функции на границах области 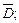
3) сравнить все полученные значения функции и выбрать из них наибольшее и наименьшее.
Если область определения функции не является замкнутой, то для нахождения наибольшего и наименьшего значений функции необходимо:
1) найти критические точки функции, принадлежащие D;
2) исследовать найденные критические точки на экстремум (локальный);
3) вычислить значения функции в точках локального максимума (минимума) и отобрать среди них наибольшее (наименьшее).
Пример 1. Исследовать на экстремум функцию
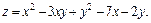
Решение. Находим частные производные первого порядка:

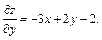
Приравниваем их к нулю, чтобы найти стационарные точки:
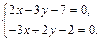
Решая систему уравнений, получим: 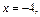
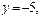 т. е.
т. е. 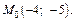
Вычисляем значения частных производных второго порядка в точке М0:
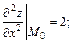
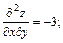
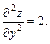
Тогда 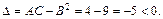 Следовательно, в точке
Следовательно, в точке 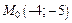 экстремума нет.
экстремума нет.
Пример 2. Найти экстремум функции 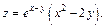
Решение.Частные производные первого порядка:
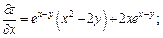
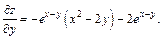
Стационарные точки:
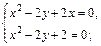
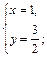
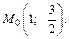
Частные производные второго порядка:
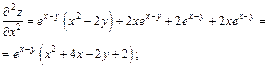
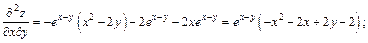

Тогда 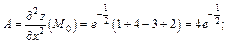
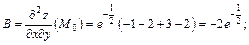
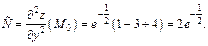
Получаем:
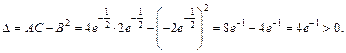
Поскольку 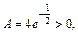 то в точке
то в точке 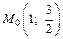 функция имеет минимум:
функция имеет минимум: 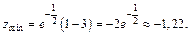
Пример 3. Найти наибольшее и наименьшее значения функции 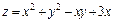 в области
в области 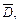 ограниченной прямыми
ограниченной прямыми 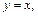
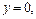
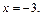
Решение. 1) Вычислим частные производные и найдем критические точки:
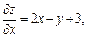
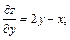
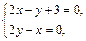
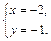
Получим: 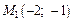 – критическая точка, принадлежащая области
– критическая точка, принадлежащая области 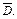
Вычислим в ней значение функции:
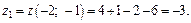
2) Исследуем функцию z на границе области  (рис. 18.4).
(рис. 18.4).
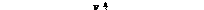
Рис. 18.4
Уравнение границы AB: 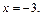 Подставляем число –3 вместо х в аналитическое задание функции:
Подставляем число –3 вместо х в аналитическое задание функции:  где
где 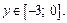
Исследуем полученную функцию, как функцию одной переменной, на наибольшее значение.
Найдем критические точки:
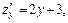
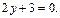
Получаем 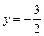 – критическая точка, при этом
– критическая точка, при этом 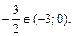
Вычисляем значение функции в точке 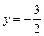 и на концах отрезка:
и на концах отрезка:
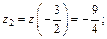

Уравнение границы BC: 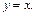 На этом участке уравнение функции имеет вид:
На этом участке уравнение функции имеет вид: 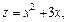 где
где 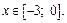
Поскольку 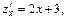 то для
то для 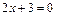 получаем критическую точку
получаем критическую точку 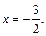 Тогда
Тогда
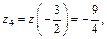
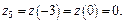
Уравнение границы AC: 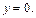 Тогда
Тогда 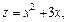 где
где 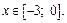 Критическая точка
Критическая точка 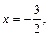 принадлежащая
принадлежащая 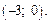
Вычисляем значение функции для 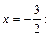
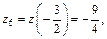
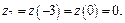
3) Из всех полученных значений z выбираем наименьшее и наибольшее:
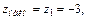
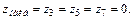
Дата добавления: 2015-09-29; просмотров: 1815;
