Б. Случай двух переменных

Более сложная задача построения по заданному набору точек в трехмерном пространстве, интерполяционной функции двух переменных решаются похожим образом. Определим, прежде всего, интерполяционный бикубический сплайн.

Пусть на плоскости задан набор из (m+1)(n+1) точек (рис 3.51)

(x_i, y_j), i=0,1,...,m; j=0,1,..,n, где х₀<x₁<...<x_m-1<x_m, y₀<y₁<...<y_n-1<y_n .

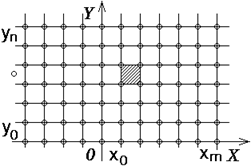
Рис. 3.51 Набор (m+1)(n+1) точек на плоскости

Добавим к каждой паре (x_i, y_j) третью координату z_ij (x_i, y_j, z_ij). Тем самым мы получаем массив (x_i, y_j, z_ij), i=0,1,...,m; j=0,1,..,n.

Прежде чем строить поверхность, проходящею через все точки заданного массива, определим функцию, графиком которой будет эта поверхность.

Интерполяционным бикубическим сплайном называется функция двух переменных S(x,y), обладающая следующими свойствами:

график этой функции проходит через каждую точку заданного массива, S(х_i,y_i)=z_i, i=0,1,...,m; j=0,1,..,n.

2) на каждом частичном прямоугольнике [x_i, x_j+1]´[y_i, y_j+1], i=0,1,...,m-1; j=0,1,..,n-1, функция представляет собой многочлен третей степени по каждой из переменных,

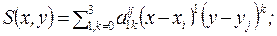
3) на всем прямоугольнике задания [x₀, x_m] ´[y₀, y_n] функция S(х, y) имеет по каждой переменной непрерывную вторую производную.

Для того чтобы построить по заданному массиву {(x_i, y_j, z_ij)} интерполяционный бикубический сплайн, достаточно определить все 16mn коэффициентов. Как и в одномерном случае, отыскание коэффициентов сплайн-функции сводится к построению решения системы линейных уравнений, связывающих искомые коэффициенты a^ij_lk.

Последняя возникает из первого и третьего условий после добавления к ним недостающих соотношений путем задания значений произвольной искомой функции в граничных узлах прямоугольника [x₀, x_m]´[y₀, y_n] (или иных соображений).

Достоинства предложенного способа несомненны: для решения линейных систем, возникающих в ходе построения сплайн-функций, существует много эффективных методов, к тому же эти системы достаточно просты; графики построенных сплайн-функций проходят через все заданные точки, полностью сохраняя первоначально заданную информацию.

Вместе с тем изменение лишь одной точки (случай на практике довольно типичный) при описанном подходе заставляет пересчитывать заново, как правило, все коэффициенты.

Однако во многих задачах исходный набор точек задается приближено и, значит, требования неукоснительного прохождения графика искомой функции через каждую точку этого набора оказывается излишним.

В этом случае используется методы сглаживания, при которых можно отказаться от требования строгого однозначного проектирования искомой кривой на координатную ось, а поверхности - на координатную плоскость.