ВЫБОР ХРАНИМЫХ ДАННЫХ
Информационный фонд системы управления должен обеспечивать получение выходных наборов данных из входных с помощью алгоритмов обработки и корректировки данных. Это возможно, если создана инфологическая модель предметной области, которая вместе с наборами хранимых данных и алгоритмами их обработки позволяет построить каноническую модель (схему) информационной базы, а затем перейти к логической схеме и, далее, к физическому уровню реализации.
Инфологической (концептуальной) моделью предметной области называют описание предметной области без ориентации на используемые в дальнейшем программные и технические средства. Однако, для построения информационной базы инфологической модели не достаточно. Необходимо провести анализ информационных потоков в системе с целью установления связи между элементами данных, их группировки в наборы входных, промежуточных и выходных элементов данных, исключения избыточных связей и элементов данных. Получаемая в результате такого анализа безызбыточная структура носит название канонической структуры информационной базы и является одной из форм представления инфологической модели предметной области.
Для анализа информационных потоков в управляемой системе исходными являются данные о парных взаимосвязях, или отношениях (т.е. есть отношение или нет отношения) между наборами информационных элементов. Под информационными элементами понимают различные типы входных, промежуточных и выходных данных, которые составляют наборы входных N1, промежуточных N2 и выходных N3 элементов данных.
Формализовано связи (парные отношения) между наборами информационных элементов отображаются в виде матрицы смежности B,под которой понимают квадратную бинарную матрицу, проиндексированную по обеим осям множеством информационных элементов
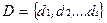 ,
,
где s - число этих элементов.
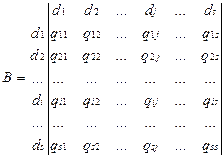
где qi j= 
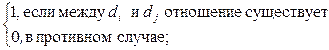
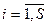 ;
; 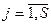
В позиции (i,j) матрицы смежности записывают „1“(т.е.qij =1), если между информационными элементами 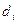 и
и 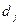 существует отношение R0, такое, что для получения значения информационного элемента
существует отношение R0, такое, что для получения значения информационного элемента 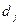 необходимо непосредственное обращение к элементу
необходимо непосредственное обращение к элементу 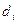 . Наличие такого отношения между
. Наличие такого отношения между 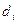 и
и 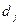 обозначают в виде
обозначают в виде 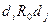 , чему соответствует qij =1, а отсутствие -
, чему соответствует qij =1, а отсутствие - 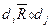 и запись „0“ в позиции (
и запись „0“ в позиции ( 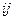 ), т.е.
), т.е. 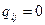 . Для простоты принимают, что каждый информационный элемент недостижим из самого себя:
. Для простоты принимают, что каждый информационный элемент недостижим из самого себя:
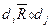 ;
; 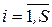 .
.
Матрице B ставится в соответствие информационный граф 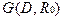 . Множеством вершин графа
. Множеством вершин графа 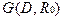 является множество D информационных элементов, а каждая дуга (di, dj) соответствует условию
является множество D информационных элементов, а каждая дуга (di, dj) соответствует условию 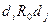 ; т.е. записи „1“ в позиции (
; т.е. записи „1“ в позиции ( 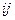 ) матрицы B.
) матрицы B.
Например, задано множество D из четырех наборов информационных элементов, т.е. 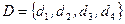 . Пусть матрица смежности B этих элементов
. Пусть матрица смежности B этих элементов
имеет вид: 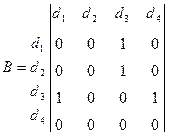 .
.
Из этой матрицы видно, что для вычисления элемента 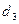 необходимо обращение к элементам
необходимо обращение к элементам 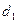 и
и 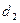 , а для получения элемента
, а для получения элемента 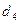 - к элементу
- к элементу 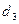 . Чтобы получить элемент
. Чтобы получить элемент 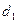 , надо обратиться к
, надо обратиться к 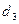 . Элемент
. Элемент 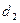 не зависит от других элементов матрицы. Информационный граф в этом простейшем случае будет соответствовать рис. 4.3.
не зависит от других элементов матрицы. Информационный граф в этом простейшем случае будет соответствовать рис. 4.3.
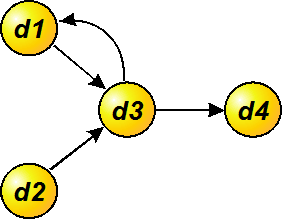
Рис.4.3 Информационный граф 
В общем случае структура графа  вследствие неупорядоченности сложна для восприятия и анализа. Составленная на основе инфологической модели, она не гарантирована от неточностей, ошибок, избыточности и транзитивности. Для формального выделения входных, промежуточных и выходных наборов информационных элементов, определения последовательности операций их обработки, анализа и уточнения взаимосвязей на основе графа
вследствие неупорядоченности сложна для восприятия и анализа. Составленная на основе инфологической модели, она не гарантирована от неточностей, ошибок, избыточности и транзитивности. Для формального выделения входных, промежуточных и выходных наборов информационных элементов, определения последовательности операций их обработки, анализа и уточнения взаимосвязей на основе графа  строят матрицу достижимости.
строят матрицу достижимости.
Матрицей достижимости M называют квадратную бинарную матрицу, проиндексированную по обеим осям множеством информационных элементов D, аналогично матрице смежности B. Запись „1“ в каждой позиции (ij) матрицы достижимости соответствует наличию для упорядоченной пары информационных элементов ( 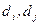 ), смыслового отношения достижимости R. Элемент
), смыслового отношения достижимости R. Элемент 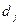 достижим из элемента
достижим из элемента 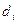 , т.е. выполняется условие
, т.е. выполняется условие 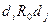 , если на графе
, если на графе 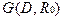 существует направленный путь от вершины
существует направленный путь от вершины 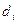 к вершине
к вершине 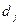 (в процессе получения значения элемента
(в процессе получения значения элемента 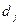 используется значение элемента
используется значение элемента 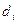 ). Если
). Если 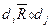 , то отношение достижимости между элементами
, то отношение достижимости между элементами 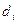 и
и 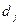 отсутствует и в позиции (ij) матрицы M записывают „0“. Отношение достижимости транзитивно, т.е. если
отсутствует и в позиции (ij) матрицы M записывают „0“. Отношение достижимости транзитивно, т.е. если 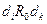 и
и 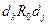 , то
, то 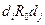 ;
; 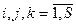 .
.
Записи „1“ в j-м столбце матрицы M соответствуют информационным элементам 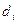 , которые необходимы для получения значений элементов
, которые необходимы для получения значений элементов 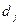 , и которые образуют множество элементов предшествования A(
, и которые образуют множество элементов предшествования A( 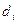 ) для этого элемента. Записи „1“ в i-ой строке матрицы M соответствуют всем элементам
) для этого элемента. Записи „1“ в i-ой строке матрицы M соответствуют всем элементам 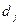 , достижимым из рассматриваемого элемента
, достижимым из рассматриваемого элемента 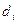 и образующим множество достижимости R(
и образующим множество достижимости R( 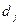 ) этого элемента. Информационные элементы, строки которых в матрице M не содержат единиц (нулевые строки), являются выходными информационными элементами, а информационные элементы, соответствующие нулевым столбцам матрицы M, являются входными. Это условие может служить проверкой правильности заполнения матриц B и M , если наборы входных и выходных информационных элементов известны. Информационные элементы, не имеющие нулевой строки или столбца, являются промежуточными.
) этого элемента. Информационные элементы, строки которых в матрице M не содержат единиц (нулевые строки), являются выходными информационными элементами, а информационные элементы, соответствующие нулевым столбцам матрицы M, являются входными. Это условие может служить проверкой правильности заполнения матриц B и M , если наборы входных и выходных информационных элементов известны. Информационные элементы, не имеющие нулевой строки или столбца, являются промежуточными.
Для полученного в примере графа (рис. 4.3) матрица M будет выглядеть так:
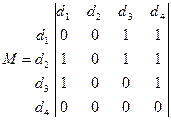
Отличие столбцов матриц M и B объясняется тем, что в матрице M учитывается смысловое отношение 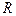 между информационными элементами, а в матрице B только непосредственное
между информационными элементами, а в матрице B только непосредственное 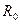 . Например, элемент
. Например, элемент 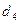 в матрице M достижим из элементов,
в матрице M достижим из элементов, 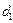 ,
, 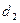 и
и 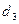 , т.е.
, т.е. 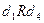 ,
, 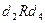 и
и 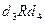 , в то время как в матрице B для этих элементов
, в то время как в матрице B для этих элементов 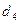 достижим только из
достижим только из 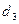 , т.е. только
, т.е. только 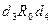 , а
, а 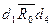 и
и 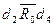 . Из анализа матрицы M следует, что элемент
. Из анализа матрицы M следует, что элемент 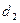 является входным,
является входным, 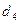 - выходным, остальные - промежуточные. На основе матрицы M строится информационный граф
- выходным, остальные - промежуточные. На основе матрицы M строится информационный граф 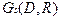 системы, структурированный по входным (
системы, структурированный по входным ( 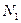 ), промежуточным (
), промежуточным ( 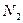 ) и выходным (
) и выходным ( 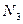 ) наборам информационных элементов, и полученный из анализа множеств элементов предшествования A(
) наборам информационных элементов, и полученный из анализа множеств элементов предшествования A( 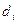 ) и достижимости R(
) и достижимости R( 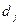 ). Граф
). Граф 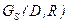 , полученный из матрицы M рассматриваемого примера, приведен на рисунке 4.4.
, полученный из матрицы M рассматриваемого примера, приведен на рисунке 4.4.
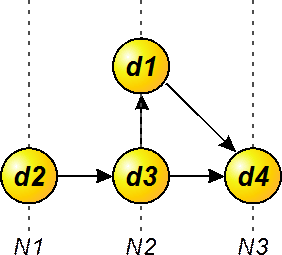
Рис.4.4 Информационный граф 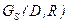
В общем случае информационный граф системы, в отличие от вычисленного графа, может иметь контуры и петли, что объясняется необходимостью повторного обращения к отдельным элементам данных.
Информационный граф системы 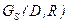 структурируется по уровням (
структурируется по уровням ( 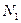 ,
, 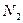 ,
, 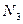 ) с использованием итерационной процедуры, что позволяет определить информационные входы и выходы системы, выделить основные этапы обработки данных, их последовательность и циклы обработки на каждом уровне. Кроме того, удаляются избыточные (лишние) дуги и элементы. Граф, получаемый после структуризации по наборам информационных элементов и удаления избыточных элементов и связей, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически неизбыточную информационную базу. Выделение наборов элементов данных по уровням позволяет объединить множество значений конечных элементов в логические записи и тем самым упорядочить их в памяти ЭВМ.
) с использованием итерационной процедуры, что позволяет определить информационные входы и выходы системы, выделить основные этапы обработки данных, их последовательность и циклы обработки на каждом уровне. Кроме того, удаляются избыточные (лишние) дуги и элементы. Граф, получаемый после структуризации по наборам информационных элементов и удаления избыточных элементов и связей, определяет каноническую структуру информационной базы. Таким образом, каноническая структура задает логически неизбыточную информационную базу. Выделение наборов элементов данных по уровням позволяет объединить множество значений конечных элементов в логические записи и тем самым упорядочить их в памяти ЭВМ.
От канонической структуры переходят к логической структуре информационной базы, а затем - к физической организации информационных массивов. Каноническая структура является также основой для автоматизации основных процессов предпроектного анализа предметных областей систем управления.
Процедуры хранения, актуализации и извлечения данных непосредственно связаны с базами данных, поэтому логический уровень этих процедур определяется моделями баз данных.
БАЗЫ ДАННЫХ
База данных определяется как совокупность взаимосвязанных данных, характеризующихся: возможностью использования для большого количества приложений; возможностью быстрого получения и модификации необходимой информации; минимальной избыточностью информации; независимостью от прикладных программ; общим управляемым способом поиска [14].
Возможность использования баз данных для многих прикладных программ пользователя упрощает реализацию комплексных запросов, снижает избыточность хранимых данных и повышает эффективность использования информационной технологии. Минимальная избыточность и возможность быстрой модификации позволяет поддерживать данные на одинаковом уровне актуальности. Независимость данных и использующих их программ является основным свойством баз данных. Независимость данных подразумевает, что изменение данных не приводит к изменению прикладных программ и наоборот.
Модели баз данных базируются на современном подходе к обработке информации, состоящем в том, что структуры данных обладают относительной устойчивостью. Действительно, типы объектов предприятия, для управления которым создается информационная технология, если и изменяются во времени, то достаточно редко, а это приводит к тому, что и структура данных, обрабатываемых эти объекты, достаточно стабильна. Поэтому возможно построение информационной базы с постоянной структурой и изменяемыми значениями данных. Каноническая структура информационной базы, отображающая в структурированном виде информационную модель предметной области, позволяет сформировать логические записи, их элементы и взаимосвязи между ними. Взаимосвязи могут быть типизированы по следующим основным видам: „один к одному“, когда одна запись может быть связана только с одной записью; „один ко многим“, когда одна запись взаимосвязана со многими другими; „многие ко многим“, когда одна и та же запись может входить в отношения со многими другими записями в различных вариантах. Применение того или иного вида взаимосвязей определило три основных модели баз данных: иерархической, сетевой реляционной.
Для пояснения логической структуры основных моделей баз данных рассмотрим такую простую задачу: необходимо разработать логическую структуру БД для хранения данных о трех поставщиках П1, П2 и П3, которые могут поставлять товары Т1,Т2 и Т3 в следующих комбинациях: поставщик П1 - все три вида товаров, поставщик П2 - товары Т1 и Т3, поставщик П3 - товары Т2 и Т3.
Сначала построим логическую модель БД, основанную на иерархическом подходе. Иерархическая модель представляется в виде древовидного графа, в котором объекты выделяются по уровням соподчиненности (иерархии) объектов (рис. 4.5).
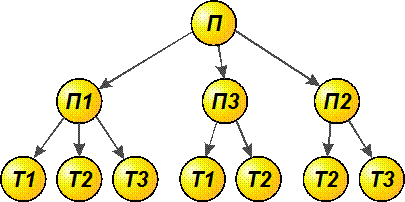
Рис.4.5 Иерархическая модель БД
На верхнем первом уровне находится информация об объекте „поставщики“ (П), на втором - о конкретных поставщиках П1, П2 и П3, на нижнем третьем уровне - о товарах, которые могут поставлять конкретные поставщики. В иерархической модели должно соблюдаться правило: каждый порожденный узел не может иметь больше одного порождающего узла (только одна входящая стрелка); в структуре может быть только один не порожденный узел (без входящей стрелки) - корень. Узлы, не имеющие входных стрелок, носят название листьев. Узел интегрируется как запись. Для поиска необходимой записи нужно двигаться от корня к листьям, т.е. сверху вниз, что значительно упрощает доступ. Иерархическая модель данных позволяет описать их структуру как на логическом, так и на физическом уровнях. Однако, из-за жесткой фиксированности взаимосвязей между элементами данных, любые изменения связей требуют изменение структуры. Принципиальным недостатком иерархической структуры является также жесткая зависимость физической и логической организации данных. Быстрота доступа в иерархической модели достигнута за счет потери информационной гибкости (за один проход по дереву невозможно, например, получить информацию о том, какие поставщики поставляют, скажем, товар Т1). Указанные недостатки ограничивают применение иерархической структуры.
В иерархической модели используется вид связи между элементами данных „один ко многим“. Если применяется взаимосвязь вида „многие ко многим“, то приходят к сетевой модели данных.
Сетевая модель базы данных для поставленной задачи представлена в виде диаграммы связей на рис.4.6.
На диаграмме указаны независимые (основные) типы данных П1, П2 и П3, т.е. информация о поставщиках, и зависимые - информация о товарах Т1, Т2 и Т3. В сетевой модели допустимы любые виды связей между записями и отсутствует ограничение на число обратных связей. Но должно соблюдаться одно правило: связь включает основную и зависимую запись.
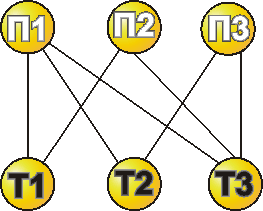
Рис.4.6 Сетевая модель БД
Сетевая модель БД, хотя и обладает большей информационной гибкостью, но, как и иерархическая, является достаточно жесткой структурой, что препятствует развитию информационной базы системы управления. При необходимости частой реорганизации информационной базы (например, при использовании настраиваемых базовых информационных технологий) применяют наиболее совершенную модель БД - реляционную, в которой отсутствуют различная между объектами и взаимосвязями.
В реляционной модели базы данных взаимосвязи между элементами данных представляются в виде двумерных таблиц, называемых отношениями. Отношения обладают следующими свойствами: каждый элемент таблицы представляет собой один элемент данных (повторяющиеся группы отсутствуют); элементы столбца имеют одинаковую природу, и столбцам однозначно присвоены имена; в таблице нет двух одинаковых строк; строки и столбцы могут просматриваться в любом порядке вне зависимости от их информационного содержания. Реляционная модель БД обладает следующими преимуществами: простотой логической модели (таблицы привычны для представления информации); гибкостью системы защиты (для каждого отношения может быть задана правомерность доступа); независимостью данных; возможностью построения простого языка манипулирования данными с помощью математически строгой теории реляционной алгебры (алгебры отношений). Собственно, наличие строгого математического аппарата для реляционной модели баз данных и обусловило её наибольшее распространение и перспективность в современных информационных технологиях.
Для приведенной выше задачи о поставщиках и товарах, логическая структура реляционной БД будет содержать три таблицы (отношения): R1 и R2, состоящие из записей о поставщиках и о товарах соответственно, и R3 - о поставках товаров поставщиками (рис. 4.7).
Учитывая широкое применение реляционных моделей баз данных в информационных технологиях (особенно экономических), дадим более подробное описание этой структуры.
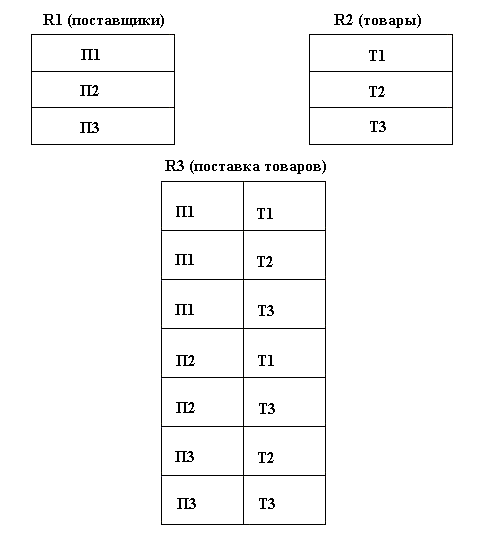
Рис 4.7 Реляционная модель БД
Дата добавления: 2015-11-06; просмотров: 2048;
