Анализ поведения переменных на основе величины погрешности

Изучив отклонения выхода сети от целевой переменной (VWNY) для шести различных входных матриц, описанных выше, можно cделать определенные выводы об относительных изменениях влияний отдельных переменных.

В столбце, обозначенном НIТ/МISS, приведены отклонения от целевого значения того прогноза, который 6-3-1 сеть сделала по исходной входной матрице. Погрешность всюду была промасштабирована так, чтобы значения располагались от -100 до 100, при этом положительный знак соответствует превышению цели, а отрицательный — недобору. Малые по абсолютной величине числа означают точный прогноз (например, апрель 1984), а большие— значительную ошибку (август 1984). Если абсолютная величина ошибки велика, скажем, больше 40, то в этом случае определить вклад отдельной переменной затруднительно. Следующие 6 столбцов таблицы содержат отклонения выхода сети от целевого значения, соответствующие шести описанным выше входным матрицам. Здесь погрешности также промасштабированы и лежат от -100 до 100. По этим данным уже можно судить о динамике отдельных переменных.

Таблица 4.6

Вклад отдельных переменных в погрешность (промасштабирован на интервал [—100,100]) за период 1984—85 гг.

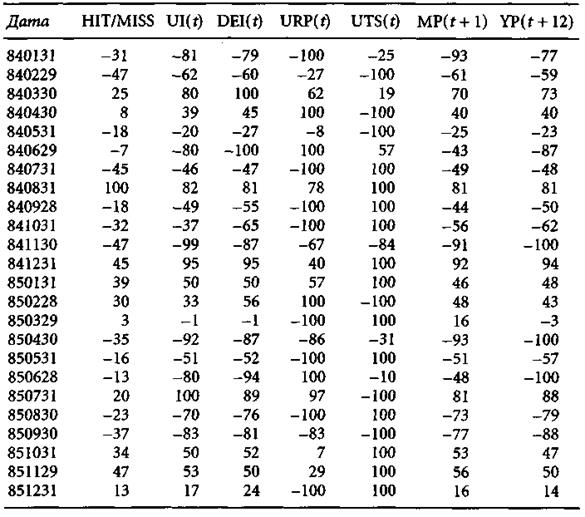
Можно заметить, что во всех случаях величина погрешности чувствительна к изменениям значений переменных, и это говорит о том, что все переменные активны. В целом, по-видимому, наибольшие погрешности связаны с переменными временной структуры и премии за риск. Замена истинных значений этих переменных их средними значениями дает относительно большую ошибку прогноза. Это замечание согласуется с результатами регрессии, согласно которым обе переменные являлись высоко значимыми. Из знака погрешностей, следует для этих переменных противоположную зависимость. Большие отрицательные погрешности для одной переменной, как правило, совпадают с большими положительными для другой, и это может указывать на то, что их вклады в погрешность в некоторой степени компенсируют друг друга. Поскольку все переменные прошли проверку на допустимость, мультиколлинеарность может быть исключена. Что касается переменных, которые по результатам регрессии были отнесены к незначимым, — например, непредвиденная инфляция, — то они, в основном, менее активны и редко дают абсолютные значения 100. Несмотря на то, что такие переменные, как показывает регрессионный анализ, в среднем мало влияют на результат, в некоторых ситуациях они могут быть очень активными. Поскольку такая маргинальная активность не улавливается регрессией, исследование чувствительности погрешности к изменениям этих якобы малозначимых переменных может продвинуть нас в понимании того, какое влияние глобальные факторы оказывают на рынок акций. Отметим, что существует метод анализа влияния переменных, основанный на решающем правиле классификации.

После того, как сеть обучена, становится возможным проследить для каждого входного решающего (determinant) вектора результаты классификации реальных доходов. Для каждого временного отрезка мы можем вычислить так называемое решающее значение классификации. Эта величина показывает, насколько оба внутренних выходных сигнала были далеки от порога, установленного для принятия решения («сила сигнала»). В нашей реализации мы просто берем среднее сил обоих сигналов. Расстояние от сигнала до порога может принимать значения от 0 до 0.5. Мы берем 0.5 за 100%, так что величина решающего значения может меняться от 0 до 100. Теперь можно определить вклад каждой из компонент входного вектора в решающую способность на взятом отрезке времени. Делается это так: временно предполагается, что значение компоненты неизвестно, и изучается изменение решающей способности на выходе. Вместо неизвестного входного значения внутрь нейронной сети вводится среднее арифметическое значение (или безусловное математическое ожидание) соответствующих входных значений. После того, как влияние всех входов вычислены, они масштабируются так, чтобы наибольшая абсолютная величина вклада у каждого входа равнялась 100. В табл. 4.7 представлен репрезентативный временной срез выходных значений.

Таблица 4.7

Классификация вкладов переменных в фактор решающей способности (KNET)

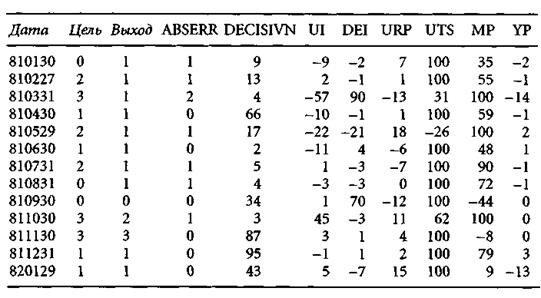
Столбец «Выход» содержит результаты классификации сети а в столбце «Цель» указан настоящий номер класса. «ABSERR» — это абсолютная ошибка классификации, т.е. расстояние до настоящего класса, а «DECISIVN» — определенная выше величина решающей способности. На всем материале не произошло ни одной грубой ошибки в классификации— величина ABSERR ни разу не превосходит двух. Переменная временной структуры имеет сильную распознающую роль. Премия за риск, наоборот, представляется лишней переменной. Месячное производство приобрело несколько большее значение, в то время как вклад переменных, выражающих инфляцию, неясен. Результаты такого анализа, которые репрезентативны для всего набора данных, не вполне согласуются с той интерпретацией роли переменных, которую мы получили при изучении погрешности. Однако это противоречие — скорее, кажущееся, поскольку KNET разбивает наблюдения на классы без учета величины и знака реального дохода.

Анализ маргинального влияния переменных имеет смысл только тогда, когда коэффициент решаемости DECISIVN велик, а фактическая ошибка классификации ABSERR (равная разности номеров действительного и спрогнозированного классов) мала. Иначе говоря, если классификация оказалась успешной, можно ожидать сильную обратную зависимость между решающей способностью и ошибкой классификации. На рис. 4.4 показано совместное распределение решающей способности (упорядочена по убыванию) и абсолютной ошибки. Хорошо видно, что число случаев неправильной классификации и величина ошибки растут с убыванием решающей способности – что и следовало ожидать.

Как уже говорилось, набор переменных, предложенный Ченом, Роллом и Россом, может быть расширен с тем, чтобы учитывалась международная торговля, например, зависимостями между так называемыми глобальными факторами и месячным доходом по Амстердамскому индексу обыкновенных акций Datastream за период с ноября 1979г. по март 1991 г. Для того чтобы учесть особенности голландского рынка, было добавлено 11 новых макроэкономических переменных (табл. 4.8), в том числе: предложение денег (М2), средний курс обмена доллар/гульден(FUS), условия торговли (TERMS).

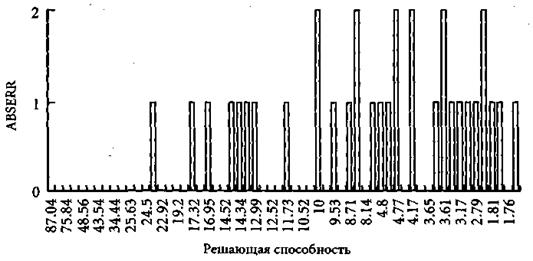
Рис. 4.4. Случаи неправильной классификации сетью (упорядочены)

Таблица 4.8

Обозначения и описания переменных

Архитектура сети такова: 17-мерный входной вектор, один скрытый слой из 9 элементов, и все эти узлы имеют непосредственные соединения с двумя бинарными элементами выходного слоя..

Установлено, например, для классификации на февраль 1989г., строка, что класс указан правильно (большой положительный доход) и решающая величина большая. Предложение денег, потребление товаров краткосрочного пользования и доход по долгосрочным государственным облигациям вносят наибольший вклад в решающую способность в том смысле, что они отчетливо подтверждают результат классификации. Наоборот, премия за риск и обменный курс валюты резко противоречат результату классификации.

Вклад переменной RETLAG (доход за время с t- 2 до t - 1) невелик, и этого следовало ожидать, поскольку изменения зависимой переменной описываются если не случайным блужданием, то, во всяком случае, мартингальным процессом. Существенная роль переменной LEVELLAG (предыдущий показатель индекса) подтверждает гипотезу о том, что уровень индекса является важным лидирующим показателем для ожидаемого дохода. То обстоятельство, что регрессия не квалифицирует эту переменную как значимую, может говорить о том, что в механизме влияния уровня индекса на доход имеется какая-то асимметрия, возможно, связанная с нелинейной обратной связью. Поведение рынка, для которого характерны возвращения к средним значениям, если оно, действительно, имеет место, неявно опровергает гипотезу эффективного рынка.

ВЫВОДЫ

В отличие от формальной модели САРМ, модель АРТ позволяет строить интуитивную стратегию управления риском от дохода по индексу путем выбора такой совокупности факторов, что несистематический риск для каждой ценной бумаги становится некоррелированным с несистематическим риском по любой другой бумаге. Нейронные сети имеют преимущество перед более традиционными методами в случаях, когда нет возможности точно описать все имеющиеся взаимосвязи, но можно выделить некоторый набор показателей, характеризующий исследуемое явление.

Данные по макроэкономическим факторам, после предварительной обработки оказываются связанными с целевой переменной (доходом на NYSE) почти идеально линейными связями, на что указывают большой коэффициент смешанной корреляции при регрессионном анализе и очень большое значение отношения Â. Выбранная архитектура сети с непосредственными связями между входами и выходами представляется для такой ситуации довольно удачной.

Однако, даже в «безрадостной» ситуации MBPN – сеть может превосходить метод OLS – регрессии в смысле показателя RMSE и коэффициента корреляции Пирсона. Более того, 6-3-1сеть даже на новых данных даёт более точный прогноз, чем оценка регрессии на уже ранее обработанных данных.

Очевидна высокая степень согласованности результатов, касающихся вклада отдельных переменных, которые дают обычная регрессия и многослойная сеть. Такое соответствие повышает уверенность в правильности результатов и одновременно говорит о том, что, по крайней мере, линейная составляющая связи между доходом по индексу и выбранным фактором улавливается нейронной сетью вполне успешно.

Остается открытым вопрос о том, в какой степени проделанные исследования поддаются обобщению

С учетом сказанного нейронные сети уже не выглядят как черные ящики. Рассмотрены два перспективных эвристических подходах к оценке динамики функциональных связей между доходами на рынке акций и переменными, описывающими состояние рынка. Один из возможных способов определения этих зависимостей состоит в том, чтобы кластеризовать их с помощью однородного или нелинейного анализа главных компонент. На полученные в результате этого кластеры можно смотреть как на возможные сценарии макроэкономического поведения. Таким образом будет подготовлена почва для применения простых правил торговли, включающих зависимость от времени.