Однородные координаты точки
Пусть М - произвольная точка плоскости с координатами х и у, вычисленными относительно заданной прямолинейной координатной системы. Однородным координатами этой точки называется любая тройка одновременно неравных нулю чисел х1, х2, х3, связанных с заданными числами х и у следующими соотношениями:
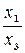 = x,
= x, 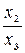 =y.
=y.
При решении задач компьютерной графики однородные координаты обычно вводятся так: произвольной точке М(х, у) плоскости ставится в соответствие точка М*(х,у,1) в пространстве (рис.3.47).
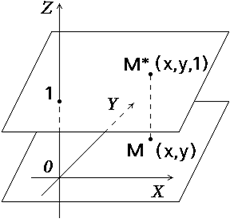
Рис. 3.47 Преобразование координат точки на плоскости в однородные координаты
Заметим, что производная точка на прямой, соединяющей начало координат, точку О(0, 0, 0), с точкой М*(х, у, 1), может быть задана тройкой чисел вида (hx, hy, h). Будем считать, что h№0.
Вектор с координатами hx, hy, h является направляющим вектором прямой, соединяющей точки О(0, 0, 0) и М*(х, у, 1). Эта прямая пересекает плоскость z=1 в точке (х, у, 1), которая однозначно определяет точку (х, у) координатной плоскости ху.
Тем самым между произвольной точкой с координатами (х, у) и множеством троек чисел вида (hx, hy, h), h№0, устанавливается (взаимно однозначное) соответствие, позволяющее считать числа hx, hy, h новыми координатами этой точки.
В проективной геометрии для однородных координат принято следующее обозначение:
х: у: 1
или, более обще,
х1: x2: x3
(напомним, что здесь непременно требуется, чтобы числа х1, х2, х3 одновременно в нуль не обращались).
Применение однородных координат оказывается удобным уже при решении простейших задач.
Рассмотрим, например, вопросы, связанные с изменением масштаба. Если устройство отображения работает только с целыми числами (или если необходимо работать только с целыми числами); то для произвольного значения h (например, h=1) точку с однородными координатами (0.5 0.1 2.5) представить нельзя. Однако при разумном выборе h можно добиться того, чтобы координаты этой точки были целыми числами. В частности, при h=10 для рассматриваемого примера имеем
(5 1 25).
Рассмотрим другой случай. Чтобы результаты преобразования не приводили к арифметическому переполнению, для точки с координатами
(80000 40000 1000)
можно взять, например, h=0,001. В результате получим (80 40 1).
Приведенные примеры показывают полезность использования однородных координат при проведении расчетов. Однако, основной целью введения однородных координат в компьютерной графике является их несомненное удобство в применении к геометрическим преобразованиям.
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости.
В самом деле, считая h =1, сравним две записи: помеченную символом * и нижеследующую, матричную:
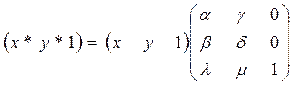
Нетрудно заметить, что после перемножения выражений, стоящих в правой части последнего соотношения, мы получим обе формулы (*) и верное числовое равенство 1=1.
Тем самым сравниваемые записи можно считать равносильными.
Элементы произвольной матрицы аффинного преобразования не несут в себе явно выраженного геометрического смысла. Поэтому чтобы реализовать то или иное отображение, то есть найти элементы соответствующей матрицы по заданному геометрическому описанию, необходимы специальные приемы. Обычно построение этой матрицы в соответствии со сложностью рассматриваемой задачи и с описанными выше частными случаями разбивают на несколько этапов.
На каждом этапе ищется матрица, соответствующая тому или иному из выделенных выше случаев А, Б, В и Г, обладающих хорошо выраженными геометрическими свойствами.
Выпишем соответствующие матрицы третьего порядка.
А. Матрица вращения (rotation)
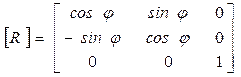
Б.Матрица растяжения (сжатия) (dilatation)
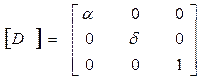
В.Матрица отражения (reflection)
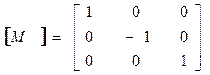
Г. Матрица переноса (translation)
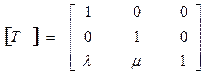
Эти матрицы трактуются как составляющие общей матрицы, преобразующей исходную матрицу А графического объекта в матрицу А* преобразованного объекта.
Общая матрица преобразования при известных j, l, a, b и m получается перемножение матриц простейших преобразований V=[R][D][M][T].
Основные свойства матричных преобразований при переходе к трехмерному (3D) преобразованию сохраняются, однако более сложной становится операция вращения, требующая задания оси вращения. Напомним, что однородное представление трехмерной точки имеет вид (hx, hy, hz, h).
Наличие точных математических моделей графических объектов позволяет относительно легко отображать их на экране монитора, а вычисленные матрицы преобразований дают возможность манипуляции этими объектами на экране, как в статике, так и в динамике.
Но далеко не всегда удается получить точное функциональное описание объекта. Чаще всего оказывается возможными вычислить только ряд точек графической фигуры. И тогда возникает задача плавного (а не прямыми) соединения этих точек для восстановления на экране изображения воспроизводимой фигуры. Эта задача в компьютерной графике решается с помощью геометрических сплайнов или сплайн-функций [46].
Сплайн-функции
Сам термин „сплайн“ происходит от английского Spline. Именно так называется, гибкая полоска стали, при помощи которой чертежники проводили через заданные точки плавные кривые. В былые времена подобный способ построения плавных обводов различных тел, таких, как, например, корпус корабля, кузов автомобиля, а потом фюзеляж или крыло самолета, был довольно широко распространен в практике машиностроения. В результате форма тела задавалась при помощи набора очень точно изготовленных сечений-плазов. Появление компьютеров позволило перейти от этого, плазово-шаблонного, метода к более эффективному способу задания поверхности обтекаемого тела. В основе этого подхода к описанию поверхностей лежит использование относительно несложных формул сплайн-функций, позволяющих восстанавливать облик изделия с необходимой точностью.
Рассмотрим сплайны, в построении которых используются кубические (в случае одномерных сплайнов - сплайновых кривых) и бикубические (в случае двумерных сплайнов - сплайновых поверхностей) многочлены. В компьютерной графике подобные сплайны применяются наиболее часто.
Достаточно типичной является следующая задача: по заданному массиву точек на плоскости (2D) или в пространстве (3D) построить кривую либо проходящую через все эти точки (задача интерполяции), либо проходящую вблизи от этих точек (задача сглаживания).
Совершенно естественно возникают вопросы: 1) в каком классе кривых искать решение поставленной задачи? и 2) как искать?
Дата добавления: 2015-11-06; просмотров: 2533;
