Базис. Координаты вектора в базисе

Определим понятие базиса на прямой, плоскости и в пространстве.

Базисом на прямой называется любой ненулевой вектор 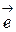на этой прямой. Любой другой вектор 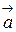, коллинеарный данной прямой, может быть выражен через вектор 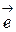в виде .

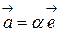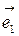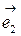Базисом на плоскости называются любых два линейно независимых вектора и этой плоскости, взятые в определенном порядке. Любой третий вектор 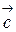, компланарный плоскости, на которой выбран базис , может быть представлен в виде .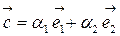

Базисом в трехмерном пространстве называются любые три некомпланарных вектора 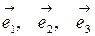, взятые в определенном порядке. Такой базис обозначается 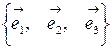. Пусть 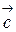‑ произвольный вектор трехмерного пространства, в котором выбран базис 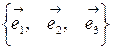. Тогда существуют числа 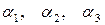такие, что:

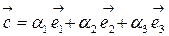
(4.5)

Коэффициенты 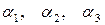называются координатами вектора 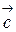в базисе 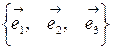, а формула (4.5) есть разложение вектора 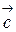по данному базису.

Координаты вектора в заданном базисе определяются однозначно. Введение координат для векторов позволяет сводить различные соотношения между векторами к числовым соотношениям между их координатами. Координаты линейной комбинации векторов равны таким же линейным комбинациям соответствующих координат этих векторов.