Базис. Декартові система координат. Дії над векторами в координатній формі
Означення. Система лінійно незалежних векторів простору, за якими можна розкласти довільний вектор, називається базисом цього простору.
Так з теореми 3 випливає, що довільні три некомпланарні вектори 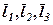 утворюють в тривимірному просторі базис, за яким, згідно з формулою (2) і зауваження до неї, можна єдиним чином розкласти довільний вектор
утворюють в тривимірному просторі базис, за яким, згідно з формулою (2) і зауваження до неї, можна єдиним чином розкласти довільний вектор 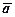 простору. Вектори
простору. Вектори 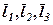 які утворюють базис називаються базисними.
які утворюють базис називаються базисними.
Будемо вважати, що базисні вектори 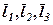 зведені до заданої О.
зведені до заданої О.
Означення.Сукупність базісу 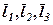 спільної точки О називають декартовою системою координат(див. рис. 11 у 2.3). Точка О називається початком координат.
спільної точки О називають декартовою системою координат(див. рис. 11 у 2.3). Точка О називається початком координат.
Іноді таку систему називають косокутною.
Числа 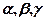 , про які згадувалось у 2.3, називають координатами вектора у заданому базисі , пишуть:
, про які згадувалось у 2.3, називають координатами вектора у заданому базисі , пишуть:
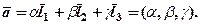
Аналогічно, на площині базис утворюють всякі два неколінеарні вектори, а всякий компланарний з ними може бути розкладений за цим базисом.
Базисним вектором на прямій лінії може бути всякий ненульовий вектор.
Із властивостей лінійних операцій над векторами випливає, що при додаванні і відніманні векторів в даному базисі додаються і віднімаються їх відповідні координати, а при множенні вектора на число множаться на це число координати вектора, тобто
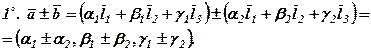
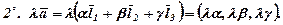
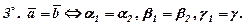
Вектори рівні, коли вони мають рівні відповідні координати.
Приклад. У деякому базисі задані своїми координатами вектори 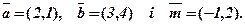 Розкласти вектор
Розкласти вектор 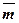 за базисом, який утворений із векторів
за базисом, який утворений із векторів 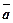 і
і 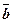 .
.
Розв’язання.Розклад вектора 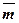 за базисом
за базисом 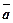 і
і 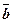 має вигляд
має вигляд
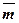 =
= 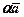 + β
+ β 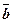 ,
,
де числа 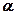 і β – невідомі. Щоб їх знайти підставимо в останню рівність координати векторів
і β – невідомі. Щоб їх знайти підставимо в останню рівність координати векторів 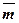 ,
, 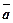 і
і 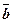 , а тоді скористаємось властивостями 10 і 20:
, а тоді скористаємось властивостями 10 і 20:
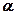 (2,1) + β(3,4) = (-1,2)
(2,1) + β(3,4) = (-1,2)
(2 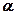 ,
, 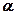 ) + (3β, 4β) = (-1,2)
) + (3β, 4β) = (-1,2)
(2 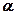 + 3β,
+ 3β, 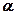 + 4β) = (-1,2)
+ 4β) = (-1,2)
За властивістю 30 про рівність векторів отримаємо систему рівнянь
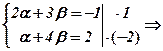 -5β = -5, β = 1, ά = -2.
-5β = -5, β = 1, ά = -2.
Отже, 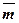 = -2
= -2 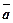 +
+ 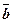 .
.
Дата добавления: 2015-09-18; просмотров: 1589;
