Векторы и линейные операции гад векторами

1)Определение вектора

Опр. Вектором называется направленный отрезок.

Обозначение .

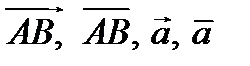Опр. Длиной вектора или модулем вектора называется длина направленного отрезка Обозначается .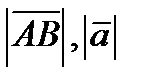

Опр. Вектор, у которого начало и конец совпадают, называется нулевым вектором. Обозначается 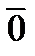. Нулевой вектор имеет произвольное направление.

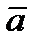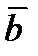Опр. Векторы и называются коллинеарными, если они лежат на одной или на параллельных прямых. Обозначение 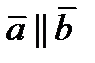.Если векторы со направлены, то 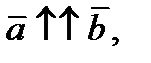противоположно направлены .

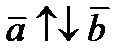Опр. Векторы называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях.

Опр. Приведем векторы к одному началу. Угол 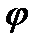между векторами это кратчайший угол, на который нужно повернуть один вектор до совмещения его со вторым. .

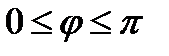Обозначение .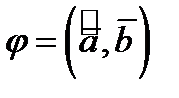

Опр. Векторы 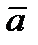и 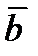называются равными 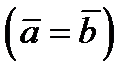, если они со направлены и их дины равны.

2)Линейные операции над векторами

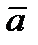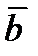Опр. Суммой векторов и называется вектор , который определяется следующим образом:

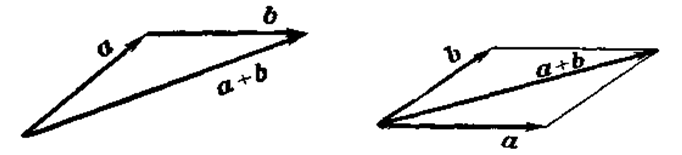
Обозначается .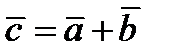

Опр.Произведением числа 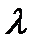на вектор 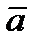называется вектор 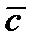, который определяется следующим образом 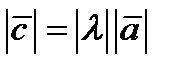, , 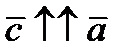есл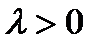и и 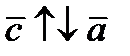, если 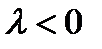, , 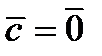ес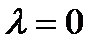ли или .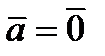

Основные свойства линейных операций

1) 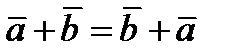следует из определения суммы векторов.

2)

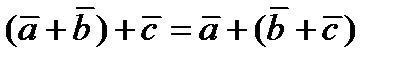
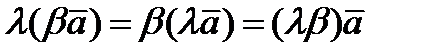
3) 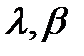– числа.

4) 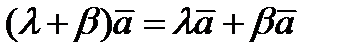. Докажите сами.

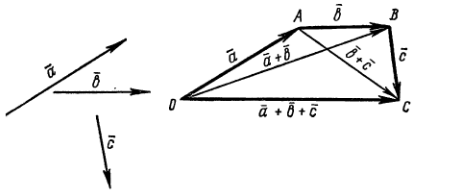
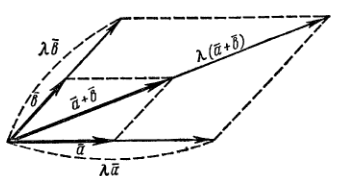
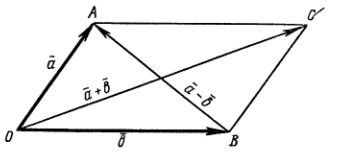
5) 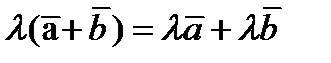. Доказательство следует из рисунка.

Теор. Есл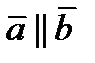и и 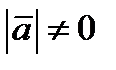, то найдется число 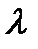такое, что .

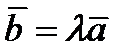Доказательство: 1) Если 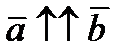, тогда 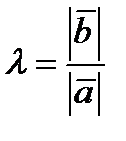. 2)Если 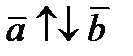,, то 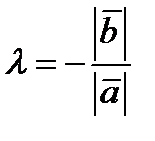.Это следует из определения произведения вектора на число.

Опр. Разностью векторов 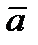и 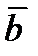называется вектор 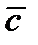такой, что 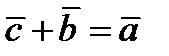. Обозначается .

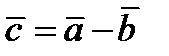§2 Линейная зависимость векторов. Базис. Система координат.

1)Линейная зависимость векторов.

Опр.Пусть даны векторы 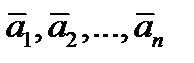. Выражени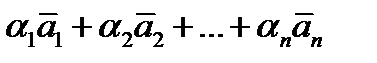е , где 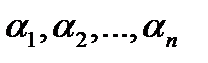– числа, называется линейной комбинацией векторов 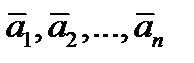,а числа 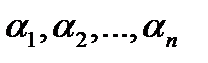- коэффициентами линейной комбинации.

Опр. Векторы 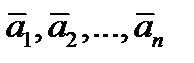называются линейно независимыми, если 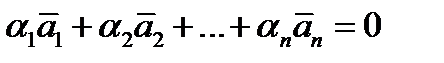в том и только в том случае, когда 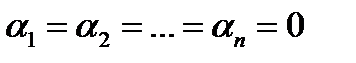в противном случае – линейно зависимыми.

Два признака линейной зависимости.

1)Если среди векторов 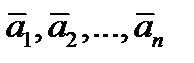есть нулевой вектор. Действительно при этом векторе может стоять любой коэффициент, а при остальных векторах коэффициенты равны 0.

2)Если среди векторов 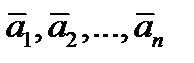часть линейно зависима, то и все векторы линейно зависимы. Действительно, если часть векторов линейно зависима, то их линейная комбинация будет равна 0, а коэффициенты при некоторых из них могут отличаться от нуля.

Теор. Для того, чтобы два вектора были линейно зависимы необходимо и достаточно, чтобы они были коллинеарные.

Доказательство.

Необходимость. Дано: векторы 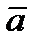и 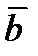линейно зависимы. Если среди них есть нулевой вектор, то векторы коллинеарные (нулевой вектор имеет произвольное направление), если векторы не равны нулю, 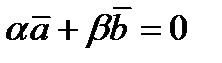, а хотя бы один коэффициент (например 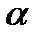) отличен от нуля. Тогда 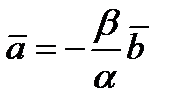. Из определения умножения вектора на число следует, что векторы 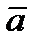и 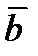коллинеарные.

Достаточность.

Дано: векторы 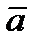и 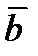коллинеарные. Если среди них есть нулевой вектор, то векторы линейно зависимы. Если нулевого вектора нет, то 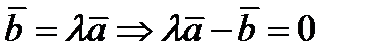.Линейная комбинация равна 0, а коэффициенты не равны нулю.

Теор. Для того чтобы три вектора были линейно зависимыми необходимо и достаточно, чтобы они были компланарными. Доказательство аналогичное предыдущему. При этом нужно рассмотреть случаи, когда среди них есть нулевой вектор и коллинеарные векторы.

Теор. Четыре вектора всегда линейно зависимы. Доказательство аналогичное. Нужно рассмотреть случаи, когда среди них есть нулевой вектор, коллинеарные и компланарные векторы.

2)Базис. Разложение по базису.

Опр. Базисом на плоскости называются два неколлинеарных векторы.

Очевидно, среди базисных векторов не может быть нулевого вектора.

Опр. Базисом в пространстве называется три некомпланарных вектора.

Теор. Любой вектор 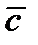компланарный базисным векторам 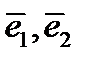может быть представлен в виде линейной комбинацией векторов ( ) .

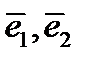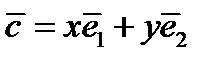Доказательство.

Так как векторы 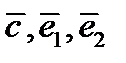компланарные, то их линейная комбинация 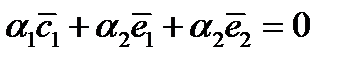, а хотя бы один из коэффициентов не равен нулю. Очевидно, что коэффициент 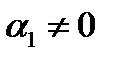, в противном случае все коэффициенты равны 0 (векторы 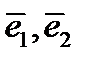линейно независимы).

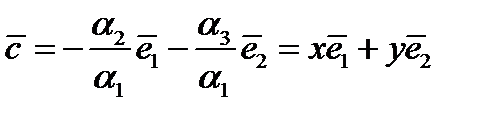. Докажем, что это представление единственное. Докажем от противного. Предположим, что не единственное. 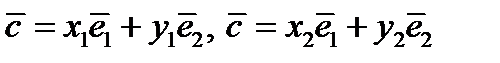. Вычитая получим 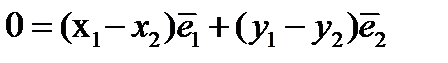.Так как векторы 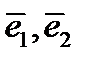линейно независимы, то .

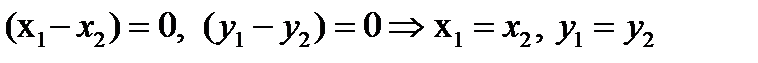Теор. Любой вектор 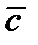в пространстве может быть представлен как линейная комбинация базисных векторов 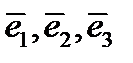. Это представление единственное.

Доказательство аналогичное.

Опр. Коэффициенты линейной комбинации в разложении вектора 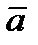по базисным векторам называются координатами вектора 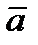в данном базисе.

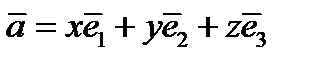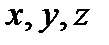, – координаты вектора. Обозначение .

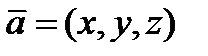Линейные операции над векторами в координатной форме.

Пусть , .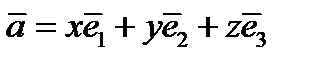

.

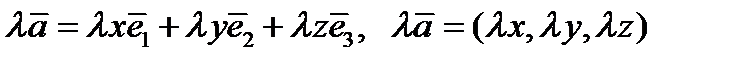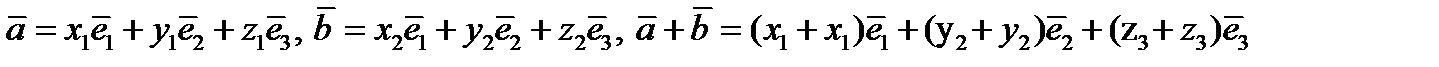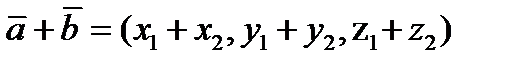
Обычно используют ортонормированный базис. Базисные векторы 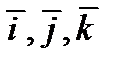взаимно перпендикулярные и .

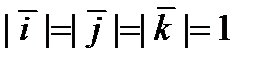3)Система координат.

Опр. Совокупность точки и базиса называется системой координат.

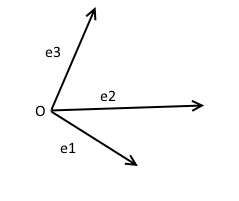
Точка О называется началом координат.

Опр. Прямые, проходящие через начало координат параллельно базисным векторам называются осями координат. Прямая параллельная вектору 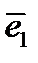– ось абсцисс, вектору 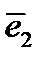– ось ординат, вектору 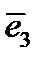– ось аппликат. Плоскости, проходящие через начало координат параллельно двум базисным векторам называются координатными плоскостями.

Задав начало координат, можно каждой точке M на плоскости или в пространстве поставить в соответствие вектор 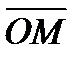. Координаты этого вектора в данном базисе 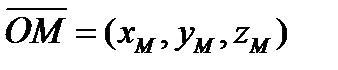называются координатами точки M в данной системе координат. Обозначается 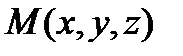. Так как вектор определяется началом и концом вектора, то вектор 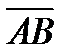можно найти как разность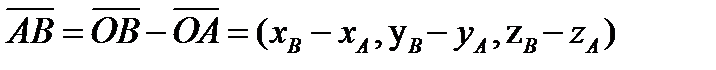

4)Проекция вектора на ось.

Опр. Прямая с заданными началом отсчета, масштабом и направлением называется осью.

Направление можно задать вектором. Проекция токи на ось это основание перпендикуляра, опущенного из точки на ось.

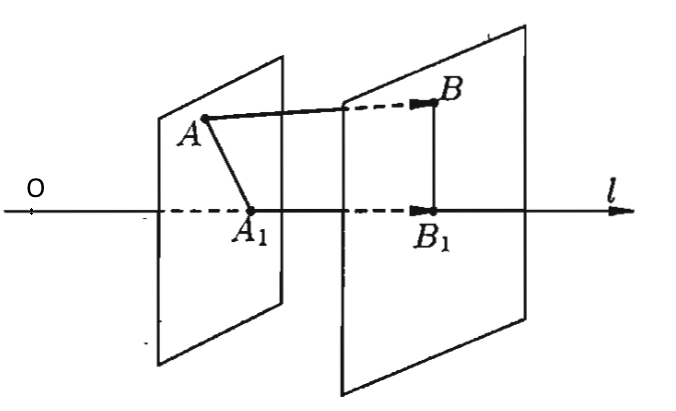
Пусть 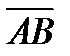– произвольный вектор

.

Проекцией вектора 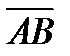на ось 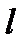называется разность 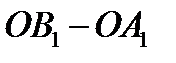.Обозначается 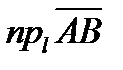. Если координаты точек 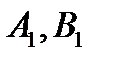обозначить 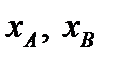, то .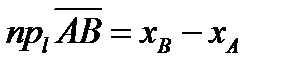

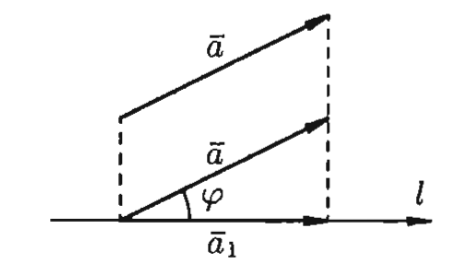
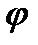– угол между вектором 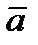и осью . .

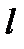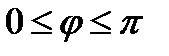Теор. Проекция вектора 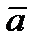на ось 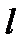равна длине вектора 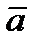, умноженной на .

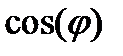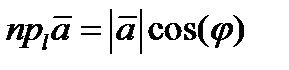
Доказательство очевидно.

Свойства проекции.

1)Проекции равных векторов на одну и ту же ось равны между собой.

2)Проекции суммы нескольких векторов на одну и ту же ось ось равна сумме их проекций на эту ось.

.

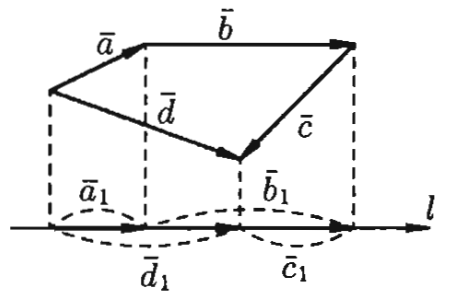
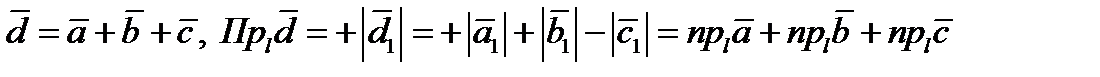3) 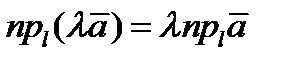. Докажите самостоятельно.

5)Прямоугольная система координат.

.

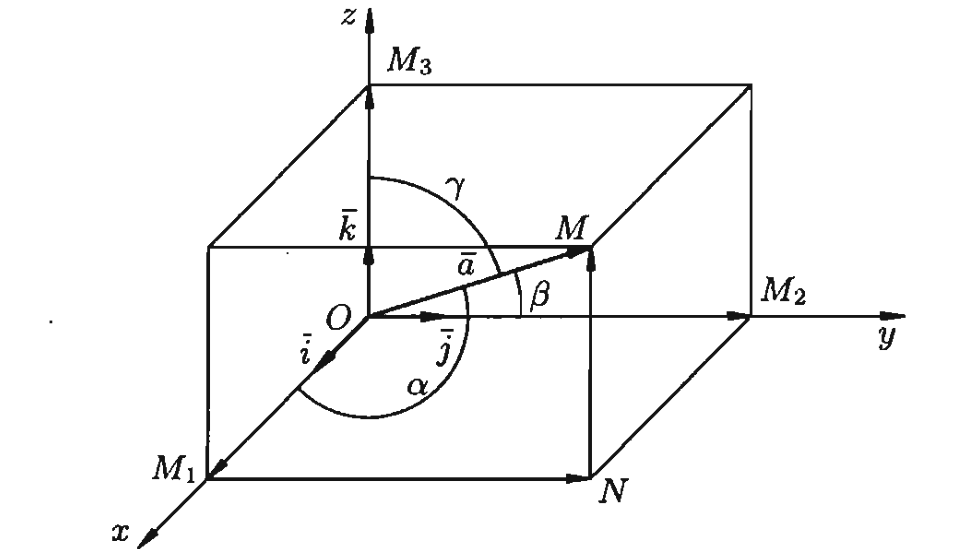
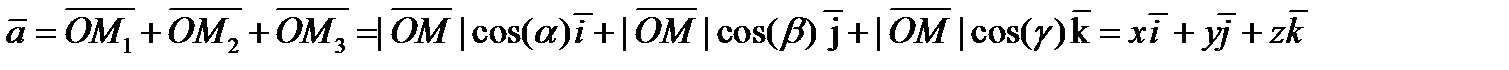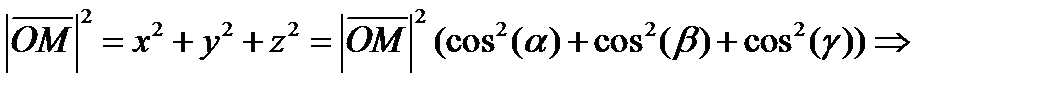
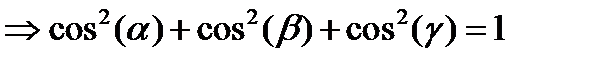– свойство направляющих косинусов.