N-мерные векторы и векторное пространство
Множества всех плоских или пространственных векторов, рассмотренных в предыдущем разделе, в которых определены операции сложения и умножения на число, являются простейшими примерами векторных пространств. Ниже обобщается понятие вектора и дается определение векторного пространства.
n-мерным вектором называется упорядоченная совокупность 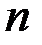 вещественных чисел, записываемых в виде
вещественных чисел, записываемых в виде 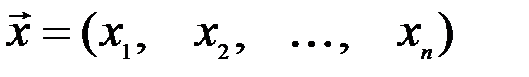 , где
, где 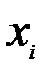 -
- 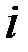 -ая компонента вектора
-ая компонента вектора 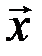 .
.
Понятие 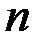 -мерного вектора широко используется в экономике. Например, если некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора
-мерного вектора широко используется в экономике. Например, если некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора 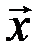 =(50, 100, 10, 50, 150), имеющего пять компонент.
=(50, 100, 10, 50, 150), имеющего пять компонент.
Два 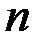 -мерных вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны, т.е.
-мерных вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны, т.е. 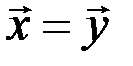 , если
, если 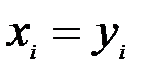 для каждого
для каждого 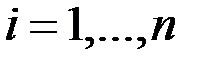 .
.
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) ¹
¹ (2, 3, 5, 0, 1).
Суммой двух векторов одинаковой размерности 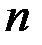 называется вектор
называется вектор 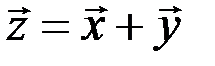 , компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е.
, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. 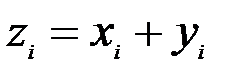 для каждого
для каждого 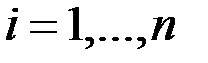 .
.
Произведением вектора на вещественное число 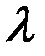 называется вектор
называется вектор 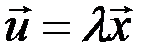 , компоненты которого равны произведению
, компоненты которого равны произведению 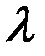 на соответствующие компоненты вектора
на соответствующие компоненты вектора 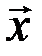 , т.е.
, т.е. 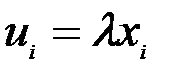 для каждого
для каждого 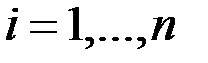 .
.
Линейные операции над любыми векторами должны удовлетворять следующим аксиомам:
1. 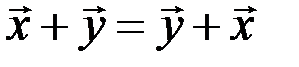 - свойство коммутативности суммы;
- свойство коммутативности суммы;
2. 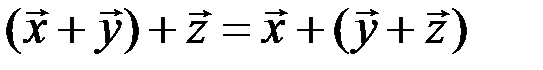 - ассоциативное свойство суммы;
- ассоциативное свойство суммы;
3. 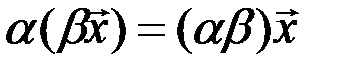 - ассоциативное относительно числового множителя свойство суммы;
- ассоциативное относительно числового множителя свойство суммы;
4. 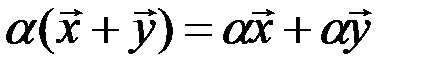 - дистрибутивное относительно векторов свойство;
- дистрибутивное относительно векторов свойство;
5. 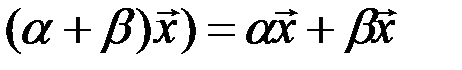 - дистрибутивное относительно суммы числовых множителей свойство;
- дистрибутивное относительно суммы числовых множителей свойство;
6.Существует нулевой вектор 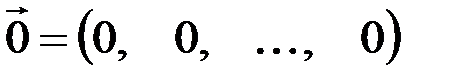 такой, что
такой, что 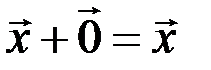 для любого вектора
для любого вектора 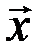 ;
;
7.Для любого вектора 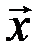 существует противоположный вектор
существует противоположный вектор 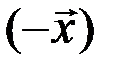 такой, что
такой, что 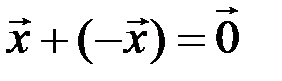 ;
;
8. 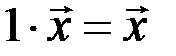 для любого вектора
для любого вектора 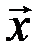 .
.
Множество векторов, в котором определены операции сложения и умножения вектора на число, удовлетворяющие приведенным выше восьми аксиомам, называется векторным пространством.
Замечание 1. Если в определении произведения вектора на число, мы ограничиваемся вещественными числами, то векторное пространство называется вещественным; если же определено умножение на любое комплексное число, то векторное пространство называется комплексным.
Замечание 2. Следует отметить, что вместо векторов 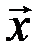 ,
, 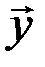 ,
, 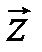 можно рассматривать элементы (объекты) любой природы. Введение операций сложения и умножения вектора (элемента) на число, удовлетворяющих приведенным выше восьми аксиомам, называется введением линейной структуры на данном множестве векторов (элементов). Поэтому векторное пространство иногда называют линейным пространством.
можно рассматривать элементы (объекты) любой природы. Введение операций сложения и умножения вектора (элемента) на число, удовлетворяющих приведенным выше восьми аксиомам, называется введением линейной структуры на данном множестве векторов (элементов). Поэтому векторное пространство иногда называют линейным пространством.
Дата добавления: 2015-09-29; просмотров: 1429;
