Примеры векторных пространств.
1. Пространство геометрических векторов на плоскости 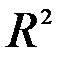 .
.
2. Пространство геометрических векторов в трехмерном пространстве 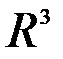 .
.
3. Множество многочленов с вещественными коэффициентами степени не выше 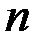 образует векторное пространство относительно операций сложения многочленов и умножения многочлена на вещественное число. Заметим для сравнения, что множество всех многочленов степени, точно равной натуральному числу
образует векторное пространство относительно операций сложения многочленов и умножения многочлена на вещественное число. Заметим для сравнения, что множество всех многочленов степени, точно равной натуральному числу 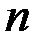 , не является векторным пространством, так как в нем не определена операция сложения элементов (сумма двух многочленов может оказаться многочленом степени ниже
, не является векторным пространством, так как в нем не определена операция сложения элементов (сумма двух многочленов может оказаться многочленом степени ниже 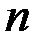 . Также множество многочленов степени не выше
. Также множество многочленов степени не выше 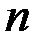 , но с положительными коэффициентами, не является векторным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа. упорядоченные совокупности
, но с положительными коэффициентами, не является векторным пространством, поскольку в этом множестве не определена операция умножения элемента на число: такие многочлены нельзя умножать на отрицательные числа. упорядоченные совокупности 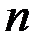 произвольных вещественных (комплексных) чисел
произвольных вещественных (комплексных) чисел 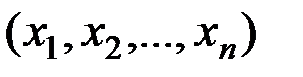 .
.
4. Множество 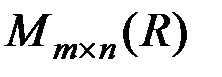 матриц одинаковых размеров образуют векторное пространство относительно операций сложения матриц и умножения матрицы на число. В частности, часто встречается и используется векторное пространство матриц-строк
матриц одинаковых размеров образуют векторное пространство относительно операций сложения матриц и умножения матрицы на число. В частности, часто встречается и используется векторное пространство матриц-строк 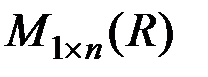 (
( 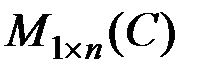 ). Для него принято другое обозначение –
). Для него принято другое обозначение – 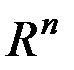 (
( 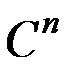 ). Элементами этого векторного пространства служат упорядоченные совокупности
). Элементами этого векторного пространства служат упорядоченные совокупности 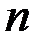 произвольных вещественных (комплексных) чисел
произвольных вещественных (комплексных) чисел 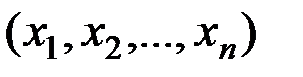 .
.
5. (Нестандартный пример). Рассмотрим множество 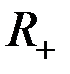 всех положительных вещественных чисел. Определим «сумму» двух элементов
всех положительных вещественных чисел. Определим «сумму» двух элементов 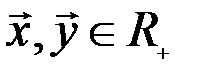 как произведение вещественных чисел
как произведение вещественных чисел 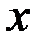 и
и 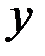 (понимаемое в обычном смысле):
(понимаемое в обычном смысле): 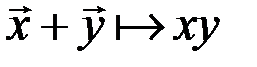 . «Произведение» элемента
. «Произведение» элемента 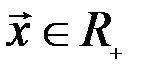 на вещественное число
на вещественное число 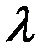 определим как возведение числа
определим как возведение числа 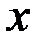 в степень
в степень 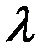 :
: 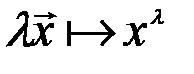 . Нулевым элементом пространства будет служить вещественное число
. Нулевым элементом пространства будет служить вещественное число 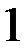 , а противоположным элементом (для данного элемента
, а противоположным элементом (для данного элемента 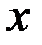 ) будет число
) будет число 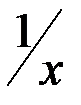 . Проверьте выполнение аксиом векторного пространства (которые в обычной записи принимают другой вид: вместо
. Проверьте выполнение аксиом векторного пространства (которые в обычной записи принимают другой вид: вместо 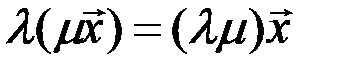 мы имеем
мы имеем 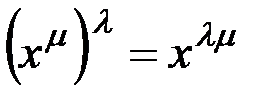 и т.д.). В этом примере, быть может, для обозначения суммы элементов пространства и для произведения элемента пространства на число предпочтительнее другие обозначения (например,
и т.д.). В этом примере, быть может, для обозначения суммы элементов пространства и для произведения элемента пространства на число предпочтительнее другие обозначения (например,  и
и  ).
).
Некоторые свойства произвольных векторных пространств.
Из определения векторного пространства следует ряд утверждений, справедливых для произвольных векторных пространств.
1. В векторном пространстве существует единственный нулевой элемент.
Доказательство. Предположим, что в пространстве существуют два нулевых элемента 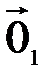 и
и 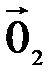 . Тогда, полагая в аксиоме 3 сначала
. Тогда, полагая в аксиоме 3 сначала 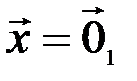 ,
, 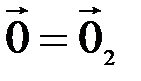 , а затем
, а затем 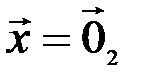 ,
, 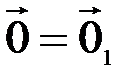 , получим два равенства
, получим два равенства 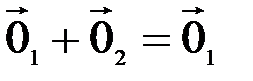 и
и 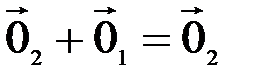 , левые части которых равны в силу аксиомы 1. Следовательно, равны и правые части этих равенств, т.е.
, левые части которых равны в силу аксиомы 1. Следовательно, равны и правые части этих равенств, т.е. 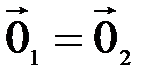 , и единственность нулевого элемента установлена.
, и единственность нулевого элемента установлена.
2. Для каждого элемента векторного пространства 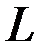 cуществует единственный противоположный элемент.
cуществует единственный противоположный элемент.
Доказательство. Предположим, что для некоторого элемента 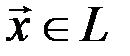 существуют два противоположных элемента
существуют два противоположных элемента 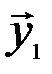 и
и 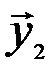 , так что
, так что 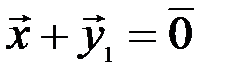 и
и 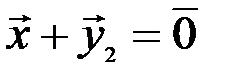 . Но тогда в силу аксиом 3, 2 и 1 получим
. Но тогда в силу аксиом 3, 2 и 1 получим
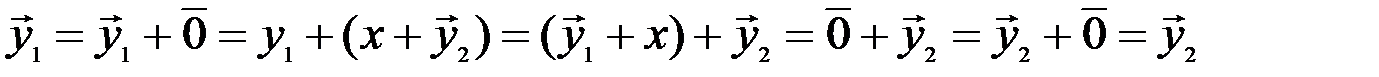 ,
,
т.е. 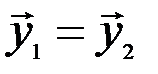 , и единственность для каждого
, и единственность для каждого 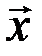 противоположного элемента доказана.
противоположного элемента доказана.
3. 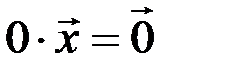 для любого элемента векторного пространства.
для любого элемента векторного пространства.
Доказательство. Пусть 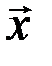 – произвольный элемент векторного пространства
– произвольный элемент векторного пространства 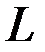 , а
, а 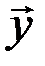 – ему противоположный. Последовательно применяя аксиомы векторного пространства (3, 4, 2, 5, 1, 7, 5, 4), будем иметь
– ему противоположный. Последовательно применяя аксиомы векторного пространства (3, 4, 2, 5, 1, 7, 5, 4), будем иметь
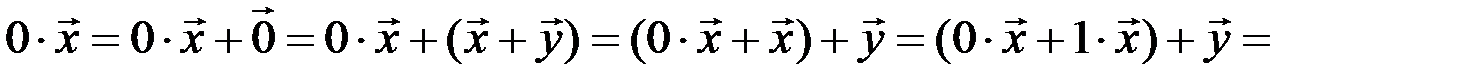
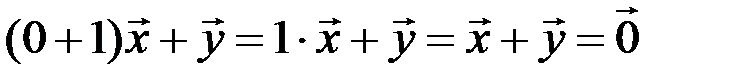 .
.
4. Для любого элемента векторного пространства 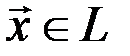 противоположный ему элемент
противоположный ему элемент 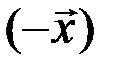 равен произведению элемента
равен произведению элемента 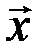 на число
на число 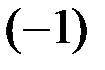 , т.е.
, т.е. 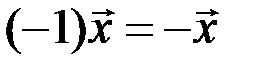
Доказательство. Имеем: 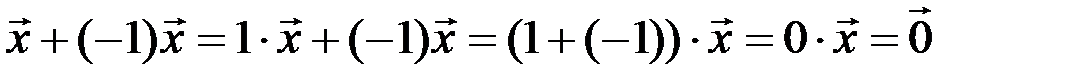 , так что элемент
, так что элемент 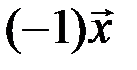 является противоположным для
является противоположным для 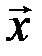 .
.
Отметим также, что из определения векторного пространства следует существование и единственность разностилюбых двух элементов векторного пространства 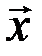 и
и 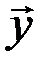 , которая определяется как элемент
, которая определяется как элемент 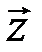 , удовлетворяющий условию
, удовлетворяющий условию 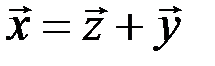 . Этим элементом служит сумма
. Этим элементом служит сумма 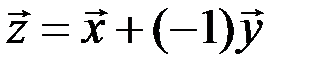 .
.
Дата добавления: 2015-09-29; просмотров: 1716;
