Линейно зависимые и независимые векторы
Вектор 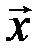 называется линейной комбинациейвекторов
называется линейной комбинациейвекторов 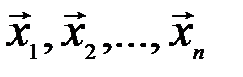 векторного пространства с коэффициентами
векторного пространства с коэффициентами 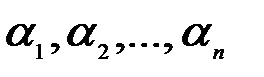 , если он равен сумме произведений этих векторов на эти коэффициенты
, если он равен сумме произведений этих векторов на эти коэффициенты
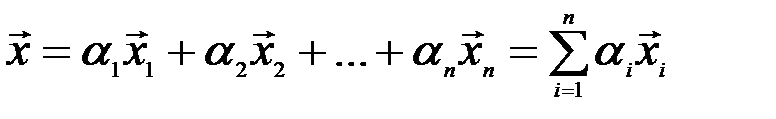 , (3.7)
, (3.7)
где 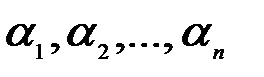 - произвольные вещественные числа.
- произвольные вещественные числа.
Линейная комбинация 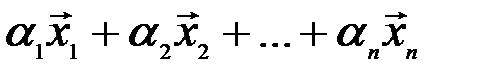 называется нетривиальной, если в ней хотя бы один из коэффициентов
называется нетривиальной, если в ней хотя бы один из коэффициентов 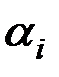 отличен от нуля.
отличен от нуля.
Линейная комбинация вида 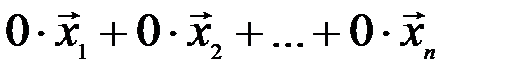 называется тривиальной. Очевидно, что она равна нулевому вектору
называется тривиальной. Очевидно, что она равна нулевому вектору  .
.
Векторы 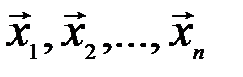 называются линейно зависимыми, если существует хотя бы одна нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е. существуют такие
называются линейно зависимыми, если существует хотя бы одна нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т.е. существуют такие 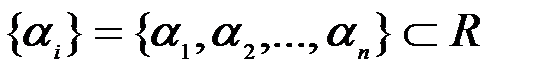 , не равные одновременно нулю, что
, не равные одновременно нулю, что
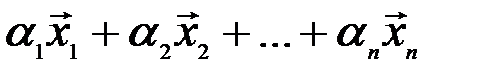 =
=  .. (3.8)
.. (3.8)
В противном случае векторы 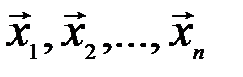 называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы 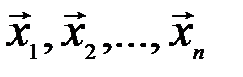 линейно независимы, если из равенства (3.8) следует, что все коэффициенты
линейно независимы, если из равенства (3.8) следует, что все коэффициенты 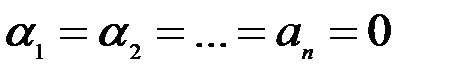 . Аналогично, векторы
. Аналогично, векторы 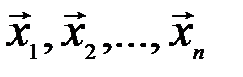 линейно зависимы, если равенство (3.8) выполняется, когда хотя бы одно из чисел
линейно зависимы, если равенство (3.8) выполняется, когда хотя бы одно из чисел 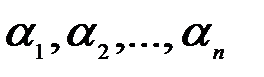 отлично от нуля.
отлично от нуля.
Примером линейно независимых векторов являются два неколлинеарных, т.е. не параллельных одной прямой, вектора 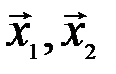 на плоскости.
на плоскости.
Действительно, условие (3.8) 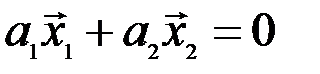 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 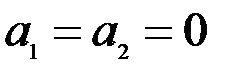 , ибо, если, например,
, ибо, если, например, 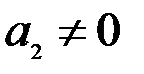 , то
, то 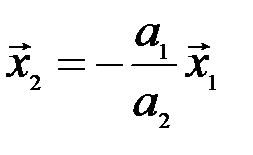 , и векторы
, и векторы 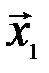 и
и 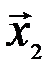 коллинеарны, что противоречит условию.
коллинеарны, что противоречит условию.
Можно показать, что если векторы 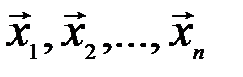 линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов линейно выражается через остальные, то все эти векторы линейно зависимы
линейно зависимы, то по крайней мере один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов линейно выражается через остальные, то все эти векторы линейно зависимы
Теорема 3.1. (критерий линейной зависимости). Для того чтобы система векторов 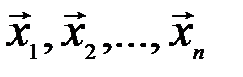 была линейно зависимой, необходимо и достаточно, чтобы, по крайней мере, один из этих векторов являлся линейной комбинацией остальных.
была линейно зависимой, необходимо и достаточно, чтобы, по крайней мере, один из этих векторов являлся линейной комбинацией остальных.
Необходимость. Пусть векторы 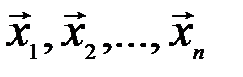 линейно зависимы, т.е. справедливо равенство
линейно зависимы, т.е. справедливо равенство
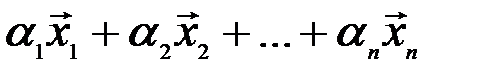 =
=  ..,
..,
в котором хотя бы одно из чисел 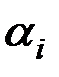 отлично от нуля. Пусть, для определенности,
отлично от нуля. Пусть, для определенности, 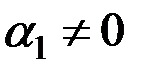 . Тогда, разделив обе части последнего равенства на
. Тогда, разделив обе части последнего равенства на 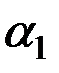 , мы можем переписать его в виде
, мы можем переписать его в виде
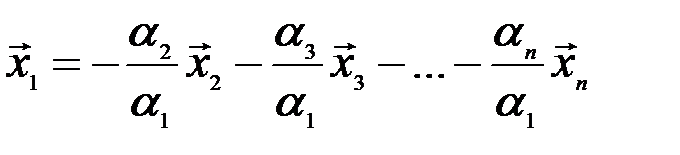 .
.
Последнее и означает, что вектор 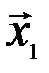 есть линейная комбинация векторов
есть линейная комбинация векторов 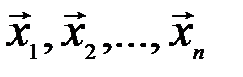 .
.
Достаточность. Пусть один из векторов (например, 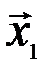 ) является линейной комбинацией остальных. Это означает, что найдутся числа
) является линейной комбинацией остальных. Это означает, что найдутся числа 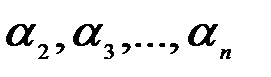 такие, что справедливо равенство
такие, что справедливо равенство
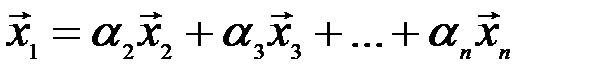 .
.
Дата добавления: 2015-09-29; просмотров: 1756;
