Анализ результатов решения линейной модели с использованием двойственных оценок
Рассмотрим задачу оптимального использования ресурсов. Запишем ее математическую модель
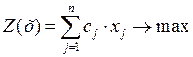
при ограничениях:
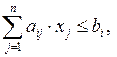
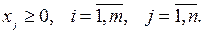
Двойственная задача имеет вид
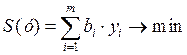
при ограничениях
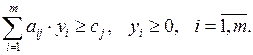
Значения переменных уi в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов системы ограничений исходной задачи на оптимальное значение ее целевой функции, т.е.
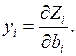
Примем 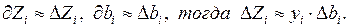
Для задачи оптимального использования сырья это уравнение показывает, что при изменении i–го ресурса оптимальный доход является линейной функцией от его приращения, причем коэффициентом служит yi – i–я компонента оптимального решения двойственной задачи.
Если yi мало, то значительному увеличению i–го ресурса будет соответствовать небольшое увеличение оптимального дохода и ценность ресурса невелика.
Если yi = 0, то при увеличении i–го ресурса оптимальный доход остается неизменным и ценность этого ресурса равна нулю. В самом деле, сырье, запасы которого превышают потребности в нем, не представляет ценности для производства и его оценку можно принять за нуль.
Если yi велико, то незначительному увеличению i–го ресурса будет соответствовать существенное увеличение оптимального дохода и ценность ресурса высока. Уменьшение ресурса ведет к существенному сокращению выпуска продукции.
Переменную yi считают некоторой характеристикой ценности i–го ресурса. В частности, при увеличении i–го ресурса на единицу ( 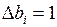 ) оптимальный доход возрастает на yi, что позволяет рассматривать yi как «условную цену», оценку единицы i–го ресурса, объективно обусловленную оценку.
) оптимальный доход возрастает на yi, что позволяет рассматривать yi как «условную цену», оценку единицы i–го ресурса, объективно обусловленную оценку.
Так как yi представляет частную производную от оптимального дохода по i–му ресурсу, то yi характеризует скорость изменения оптимального дохода при изменении i–го ресурса.
С помощью yi можно определить степень влияния ограничений на значение целевой функции. Предельные значения (нижняя и верхняя границы) ограничений ресурсов, для которых yi остаются неизменными, определяются следующим образом.
Пределы уменьшения (нижняя граница) определяются по тем 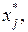 для которых соответствующие dij >0:
для которых соответствующие dij >0:
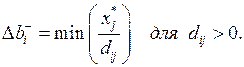
Пределы увеличения (верхняя граница) определяются по тем 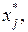 для которых dij < 0:
для которых dij < 0:
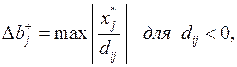
где 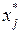 – значение переменной в оптимальном решении;
– значение переменной в оптимальном решении;
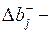 величина уменьшения i-го ресурса;
величина уменьшения i-го ресурса;
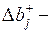 величина увеличения i-го ресурса;
величина увеличения i-го ресурса;
dij – коэффициенты столбцов свободных переменных в оптимальном плане (коэффициенты структурных сдвигов, элементы обратной матрицы к базису оптимального плана).
Если в план включаются новые виды продукции, то их оценка находится по формуле
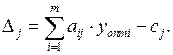
Если 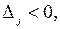 то новый вид продукции улучшает план. При
то новый вид продукции улучшает план. При 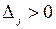 нецелесообразно включать новый вид продукции.
нецелесообразно включать новый вид продукции.
Математическая постановка задачи целочисленного линейного программирования (задача с неделимостями)может быть сформулирована в следующем виде:
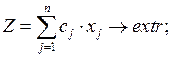
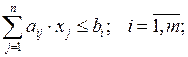 (2.1)
(2.1)
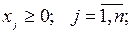
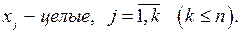
Система (2.1) с точки зрения зависимостей ничем не отличается от задачи линейного программирования (1.1) и ей подобных. Единственное отличие состоит в том, что в ней есть строка, где 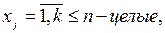 которая оказывает существенное влияние на решение задачи и значительно его усложняет. Число целочисленных переменных k удовлетворять одному из двух вариантов.
которая оказывает существенное влияние на решение задачи и значительно его усложняет. Число целочисленных переменных k удовлетворять одному из двух вариантов.
Если k = n, где n – общее число переменных, то в ответе все переменные должны быть только целыми; в этом случае задачу называют полностью целочисленной. Если k < n, т.е. в ответе только k переменных должны быть целыми, а остальные в заданных граничных условиях могут принимать любые значения, то задачу называют частично целочисленной. Класс таких задач наиболее широк. Например, задачей частично–целочисленного линейного программирования является основная производственная задача, когда часть видов продукции дискретна, а часть – непрерывна. Следует отметить, что для решения задачи все целочисленные переменные обязательно должны иметь верхнюю границу.
Модель (2.1) естественно интерпретировать, например, в следующих терминах. Пусть через 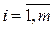 обозначены производственные факторы, через
обозначены производственные факторы, через 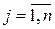 – виды конечной продукции.
– виды конечной продукции.
Обозначим далее:
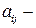 количество факторов i, необходимое для производства единицы продукции j;
количество факторов i, необходимое для производства единицы продукции j;
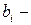 наличные ресурсы фактора i;
наличные ресурсы фактора i;
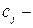 прибыль, получаемая от единицы продукта j.
прибыль, получаемая от единицы продукта j.
Пусть продукты j являются неделимыми, т.е. физический смысл имеет лишь их целое неотрицательное количество («штуки»). Предположим, что требуется составить производственную программу, обеспечивающую максимум суммарной прибыли и не выводящую за пределы данных ресурсов. Обозначая через xj искомые объемы выпуска продукции, мы сводим эту задачу к модели (2.1).
Как следует из гл. 1, непрерывные задачи обычно решаются симплекс-методом с построением симплекс-таблиц, при этом каждой итерации соответствует своя симплекс-таблица, на основании ряда признаков, по которым можно получить ответы на вопросы: имеет ли задача допустимое решение и является ли решение данной итерации допустимым или оптимальным? При наличии решения задачу решают до тех пор, пока не выявятся определенные признаки (решение является допустимым, если удовлетворяется один признак, и оптимальным, если удовлетворяются оба признака). Для целочисленных задач такие признаки отсутствуют, поэтому по задаче нельзя судить о том, имеет ли она вообще допустимое решение и является ли полученное решение оптимальным.
Программа MS Excel позволяет находить точное решение задач целочисленного линейного программирования. При этом общий порядок подготовки и решения полностью аналогичен рассмотренному ранее в гл. 1 процессу решения задач линейного программированию. Для оценки точности получаемых решений можно сравнить полученные различными способами оптимальные решения отдельных практических задач. Рассмотрим решение целочисленной задачи с помощью программы MS Excel на следующем примере.
Требуется определить, в каком количестве надо выпускать продукцию четырех типов A, B, C и D, для изготовления которой требуются ресурсы трех типов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены в таблице 2.1.
Таблица 2.1
Исходные данные задачи
| Ресурс | Продукция | Наличие ресурса | |||
| A (х1) | B (х2) | C (х3) | D (х4) | ||
| Трудовые | |||||
| Сырье | |||||
| Финансы | |||||
| Прибыль | – |
Составим математическую модель, для чего введем следующие обозначения:
xj – количество выпускаемой продукции j – го типа, 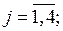
bi – количество располагаемого ресурса i – го вида, 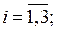
aij – норма расхода i – го ресурса для выпуска единицы продукции j – го типа;
cj – прибыль, получаемая от реализации единицы продукции j – го типа.
Тогда математическая модель задачи будет иметь вид:
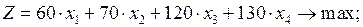
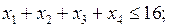
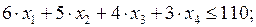 (2.2)
(2.2)
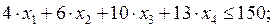
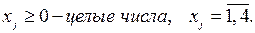
Для решения поставленной задачи выполним следующие подготовительные действия:
1. Внесем необходимые надписи в ячейки A1:E1, A2:A8, B5, B3:G3, F5:I5. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой задачи линейного программирования.
2. В ячейки B4:E4введем значения коэффициентов целевой функции: с1 = 60, с2 = 70, с3 = 120, с4 = 130.
3. В ячейку F4введем формулу: =СУММПРОИЗВ(B2:E2;B4:E4), которая представляет целевую функцию.
4. В ячейки B6:E8 введем значения коэффициентов ограничений.
5. В ячейки H6:H8введемзначения правых частей ограничений: b1 = 16, b2 = 110, b3 = 150.
6. В ячейку F6 введем формулу: =СУММПРОИЗВ($B$2:$E$2;B6:E6), которая представляет левую часть первого ограничения.
7. Скопируем формулу, введенную в ячейку F6,в ячейки F7и F8.
8.В ячейку I6введем формулу: =I6 – F6, которая представляет разность между правой частью и левой частью.
9.Скопируем формулу, введенную в ячейку I6,в ячейки I7и I8.
Внешний вид рабочего листа Excel с исходными данными для решения рассматриваемой задачи имеет следующий вид (рис. 2.1):
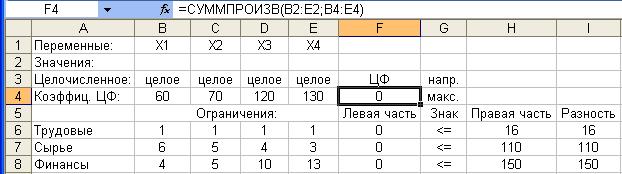
Рис. 2.1. Исходные данные для решения задачи
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис Þ Поиск решения...
После появления диалогового окна Поиск решенияследует выполнить следующие действия:
1. В поле с именем Установить целевую ячейку:ввести абсолютный адрес ячейки $F$4.
2. Для группы Равной:выбрать вариант поиска – максимальному значению.
3. В поле с именем Изменяя ячейки:ввести абсолютный адрес ячеек $B$2:$E$2.
4. Добавить3 ограничения, условия неотрицательности и целочисленности переменных. С этой целью выполнить следующие действия:
· для задания ограничений в исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить(рис. 2.2).
· в появившемся дополнительном окне выбрать диапазон ячеек $F$6:$F$8,который должен отобразиться в поле с именем Ссылка на ячейку;
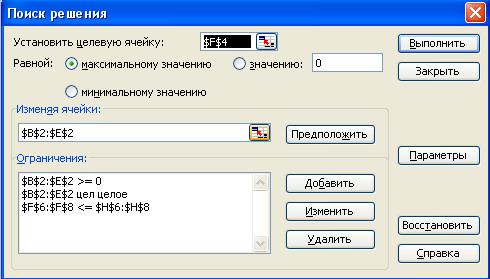
Рис. 2.2. Диалоговое окно Поиск решения
· в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство «<=»;
· в качестве значения правой части ограничения выбрать диапазон ячеек $H$6:$H$8;
· для добавления ограничений в дополнительном окне нажать кнопку с надписью Добавить(рис. 2.3);
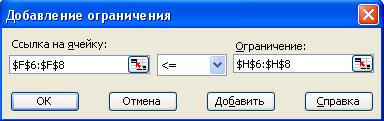
Рис. 2.3. Дополнительное окно Добавление ограничения
5. Добавить ограничения на допустимые значения и целочисленности переменных. С этой целью выполнить следующие действия:
· в дополнительном окне выбрать диапазон ячеек $B$2:$E$2, который должен отобразиться в поле с именем Ссылка на ячейку;
· в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство «³»;
· в качестве значения правой части ограничения в поле с именем Ограничение:ввести значение 0;
· в дополнительном окне выбрать диапазон ячеек $B$2:$E$2, который должен отобразиться в поле с именем Ссылка на ячейку;
·в качестве знака ограничения из выпадающего списка выбрать строку «цел»;
·в качестве значения правой части ограничения в поле с именем Ограничение:оставить без изменения вставленное программой значение «целое»;
· для добавления последнего ограничения в дополнительном окне нажать кнопку ОК.
6. В дополнительном окне параметров поиска решения следует выбрать отметки Линейная модельи Неотрицательные значения(рис. 2.4).
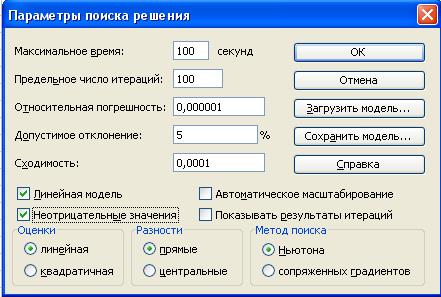
Рис. 2.4. Параметры мастера поиска решения
7. После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить.По завершении оптимизации откроется диалоговое окно Результаты поиска решения(Рис. 2.5):
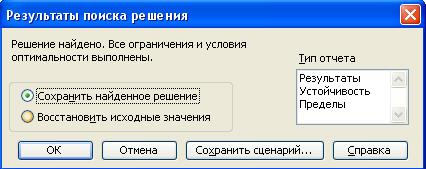
Рис. 2.5. Диалоговое окно Результаты поиска решения
8. Установим переключатель Значения параметровв положение Сохранить найденное решение,после чего щелкнем по кнопке ОК.После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рисунке 2.6.
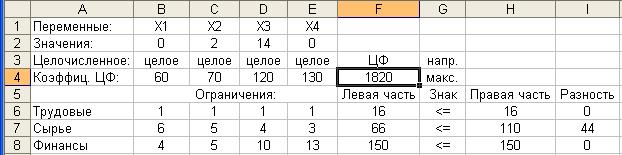
Рис. 2.6. Результат количественного решения задачи
Результатом решения задачи являются найденные оптимальные значения переменных: х1 = 0; х2 = 2; х3 = 14; х4 = 0, которым соответствует значение целевой функции: ¦opt = 1820.
Анализ найденного решения показывает, что для обеспечения максимальной прибыли следует выпускать 2 единицы продукции В и 14 единиц продукции D. При этом имеющиеся трудовые и финансовые ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырья S2 = 44, значит, имеются излишки сырья.
Сравнительные данные для непрерывного и целочисленного решений приведены в таблице 2.2.
Таблица 2.2
| Решение | х1 | х2 | х3 | х4 | ЦФ | S1 | S2 | S3 | |
| Непрерывное | 1,67 | 14,33 | 42,67 | ||||||
| ЦЧ решение |
Примечание: обозначения S1, S2 и S3 означают соответственно недоиспользование трудовых, сырьевых и финансовых ресурсов.
Из этой таблицы вытекает следующее:
îв целочисленном решении появился выпуск продукции В (х2), которого не было в непрерывном решении. Такое изменение непрерывного решения для выполнения требований целочисленности не является очевидным;
îцелевая функция как в непрерывном, так и в целочисленном решениях аналогичны. Однако требование целочисленности, как и любое дополнительное требование, может ухудшить целевую функцию;
îнедоиспользование сырьевого ресурса в целочисленном решении больше (S2 = 44), чем в непрерывном решении (S2 = 42,67).
Таким образом, если линейную задачу с требованием целочисленности неизвестных решить симплексным методом, то решение, как правило, не является целочисленным. Если попытаться результаты такого решения округлить до ближайшего целого числа, то результат может оказаться далеким от решения и не принадлежать области допустимых решений.
Дата добавления: 2015-11-18; просмотров: 2256;
