ЗАКРЫТАЯ ТРАНСПОРТНАЯ ЗАДАЧА
Рассмотрим закрытую транспортную задачу. Обозначим через xij – количество груза, перевозимого из пункта Ai в пункт Bj. Условия закрытой транспортной задачи запишем в распределительную таблицу, которую будем использовать для нахождения решения.
Математическая модель закрытой транспортной задачи имеет вид
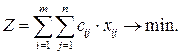
Систему ограничений получаем из следующих условий задачи:
а) все грузы должны быть перевезены, т.е.
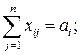
б) все потребности должны быть удовлетворены, т.е.
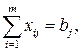
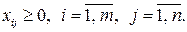
Оптимальным решением задачи является матрица
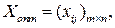
удовлетворяющая системе ограничений и доставляющая минимум целевой функции. Транспортная задача, как задача линейного программирования, может быть решена симплексным методом, однако наличие большого числа переменных и ограничений делает вычисления громоздкими.
Рассмотрим каждый из приведенных выше этапов.
Условия задачи и ее исходное опорное решение будем записывать в распределительную таблицу. Клетки, в которых поместим грузы, называются занятыми, им соответствуют базисные переменные опорного плана. Остальные клетки – незанятые, или пустые, им соответствуют свободные переменные. В верхнем правом углу каждой клетки будем записывать тарифы. Существует несколько способов нахождения опорного плана:
· метод северо-западного угла;
· метод минимальной стоимости;
· метод двойного предпочтения и т.д.
План составляется последовательным заполнением по одной клетке в таблице перевозок так, что каждый раз либо полностью удовлетворяется потребность одного из потребителей, либо полностью вывозится груз от некоторого поставщика. В теории доказывается, что базисное решение системы ограничений (из m + n уравнений с m´ n переменными) в условиях транспортной задачи имеет m + n – 1 базисных переменных, т.е. заполненных клеток (ее ранг равен m + n – 1), поэтому, совершив m + n – 1 указанных шагов, получим первый опорный план. Различие метода северо-западного угла и различных модификации метода наименьшей стоимости отыскания первого опорного плана состоит в различии способов выбора последовательности заполнения клеток.
Метод северо-западного угла. В соответствии с этим методом загрузка клеток (распределение объемов пунктов отправления по пунктам назначения) начинается с верхней левой клетки х11 («северо-западная» часть таблицы), продолжается вниз и вправо (по диагонали) и заканчивается в клетке неизвестного xmn.
Метод минимальной (наименьшей) стоимости (минимального тарифа, минимального элемента). Исходный опорный план, построенный методом северо-западного угла, как правило, оказывается весьма далеким от оптимального, так как при его определении совершенно игнорируется величины затрат cij. Поэтому требуются в дальнейших расчетах много итераций для достижения оптимального плана. Число итераций можно сократить, если исходный план строить по более рациональному правилу «минимального элемента». Сущность его состоит в том, что на каждом шаге заполняется клетка с наименьшей величиной cij. Если такая клетка не единственная, то лучше заполнять ту, по вертикали или по горизонтали которой встречаются большие cij, а в принципе заполняется любая из них.
Пусть это будет клетка (i, j). Запишем в эту клетку xij = min(ai, bj). Если ai < bj, то запасы поставщика Ai исчерпаны, а потребность Bj стала 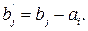 Поэтому, не принимая более во внимание i-ю сроку, снова ищем клетку с наименьшей стоимостью перевозок и заполняем ее с учетом изменившихся потребностей. Для случая ai > bj из рассмотрения исключается j-й столбец, а запасы Ai полагаются равными
Поэтому, не принимая более во внимание i-ю сроку, снова ищем клетку с наименьшей стоимостью перевозок и заполняем ее с учетом изменившихся потребностей. Для случая ai > bj из рассмотрения исключается j-й столбец, а запасы Ai полагаются равными  Продолжаем этот процесс до тех пор, пока все запасы не будут исчерпаны, а все потребности – удовлетворены. Необходимо отметить, что при наличии в таблице клеток с одинаковыми тарифами, планы, полученные с помощью этого метода, могут быть разными, однако они, несомненно, ближе к оптимальному, чем план, составленный по методу северо-западного угла.
Продолжаем этот процесс до тех пор, пока все запасы не будут исчерпаны, а все потребности – удовлетворены. Необходимо отметить, что при наличии в таблице клеток с одинаковыми тарифами, планы, полученные с помощью этого метода, могут быть разными, однако они, несомненно, ближе к оптимальному, чем план, составленный по методу северо-западного угла.
Метод двойного предпочтения. В модификации метода минимальной стоимости «двойного предпочтения» отмечают клетки с наименьшими стоимостями перевозок сначала по каждой строке, а затем по каждому столбцу. Клетки, имеющие две отметки, заполняют в первую очередь, затем заполняют клетки с одной отметкой, а данные о нераспределенном грузе записывают в неотмеченные клетки с наименьшими стоимостями. При этом из двух клеток с одинаковой стоимостью перевозок предпочтение отдается клетке, через которую осуществляется больший объем перевозок.
Пример составления начального распределения методом северо-западного угла показан в табл. 3.1.
Таблица 3.1
| Поставщики | Потребители | Запасы, ai | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребности, bj | 280 = 280 |
Порядок заполнения клеток: (А1;В1), (А1;В2), (А2;В2), (А2;В3), (А3;В3), (А3;В4). Число занятых клеток равно m + n – 1 = 3 + 4 – 1 = 6. Суммарные затраты на реализацию данного плана перевозок составят
Zопт = 4·30 + 5·30 + 3·70 + 6·30 + 7·10 + 4·110 = 1170.
Пример начального распределения методом наименьших стоимостей для тех же исходных данных, что и ранее, представлен в табл. 3.2.
Таблица 3.2
| Поставщики | Потребители | Запасы, ai | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 4 | 5 | 2 40 | 3 20 | |
| А2 | 1 30 | 3 | 6 | 2 70 | |
| А3 | 6 | 2 100 | 7 | 4 20 | |
| Потребности, bj | 280 = 280 |
Порядок заполнения клеток: (А2;В1), (А3;В2), (А2;В4), (А1;В3), (А1;В4), (А3;В4). Суммарные затраты на реализацию данного плана перевозок составляют
Zопт = 1·30 + 2·100 + 2·70 + 2·40 + 3·20 + 4·20 = 590.
Пример начального распределения методом двойного предпочтения для тех же исходных данных, что и ранее, представлен в табл. 3.3.
Таблица 3.3
| Поставщики | Потребители | Запасы, ai | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 4 | 5 | 2 40 | 3 20 | |
| А2 | 1 30 | 3 | 6 | 2 70 | |
| А3 | 6 | 2 100 | 7 | 4 20 | |
| Потребности, bj | 280 = 280 |
Порядок заполнения клеток: (А2;В1), (А3;В2), (А1;В3), (А2;В4), (А1;В4), (А3;В4). Суммарные затраты на перевозки, представленные в табл. 3.3, составляют
Zопт = 1·30 + 2·100 + 2·40 + 2·70 + 3·20 + 4·20 = 590.
Следовательно, опорные планы, построенные методами наименьших стоимостей, значительно ближе к оптимальному плану, чем план, составленный по методу северо-западного угла.
При распределении грузов может оказаться, что количество занятых клеток меньше, чем m + n – 1. Такой план называется вырожденным. В этом случае недостающее их число заполняется клетками с нулевыми поставками 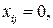 такие клетки называют условно занятыми.
такие клетки называют условно занятыми.
Нулевые поставки помещают в незанятые клетки с учетом наименьшего тарифа таким образом, чтобы в каждых строке и столбце было не менее чем по одной занятой клетке.
Дата добавления: 2015-11-18; просмотров: 3491;
