Методика решения задачи о назначении в MS EXCEL
Для решения задачи о назначении с помощью программы MS Excel необходимо задать конкретные значения параметрам. Для определенности рассмотрим вариант задачи о назначении в форме минимизации общих затрат на выполнение работ. В этом случае в качестве кандидатов рассмотрим сотрудников некоторой фирмы: Андреев, Бубнов, Васильев, Григорьев и Дмитриев, а в качестве работ – вакантные должности в этой фирме: менеджер, программист, бизнес-аналитик, маркетолог и руководитель проектов. Затраты 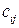 на замещение должностей кандидатами, связанные с необходимостью их предварительного обучения и стажировки, заданы в форме следующей таблицы.
на замещение должностей кандидатами, связанные с необходимостью их предварительного обучения и стажировки, заданы в форме следующей таблицы.
Таблица 2.4
Затраты на замещение должностей кандидатами, тыс. тнг.
| Андреев | Бубнов | Васильев | Григорьев | Дмитриев | |
| Менеджер | |||||
| Программист | |||||
| Бизнес-аналитик | |||||
| Маркетолог | |||||
| Руководитель проектов |
Соответствующая математическая постановка рассматриваемой задачи о назначении может быть записана в следующем виде:
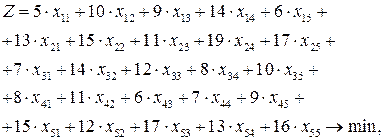 (2.14)
(2.14)
где множество допустимых альтернатив формируется следующей системой ограничений типа равенств:
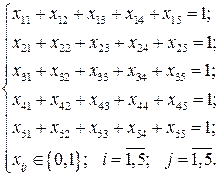 (2.15)
(2.15)
Первые 5 ограничений данной задачи соответствуют общему ограничению (2.11), следующие 5 ограничений – общему ограничению (2.12), а последнее ограничение – общему ограничению (2.13).
Для решения сформулированной задачи о назначении с помощью программы MS Excel выполним следующие подготовительные действия:
1. Внесем необходимые надписи в ячейки A7:A13, B1, G1, B7:G7,как это изображено на рис. 2.7. Следует отметить, что конкретное содержание этих надписей не оказывает никакого влияния на решение рассматриваемой задачи о назначении.
2. В ячейки B2:F6введем значения коэффициентов целевой функции (см. табл. 2.4).
3. В ячейку G2введем формулу: =СУММПРОИЗВ(B2:F6;B8:F12), которая представляет целевую функцию Z.
4. В ячейку G8введем формулу: =СУММ(B8:F8), которая представляет первое ограничение из приведенной системы ограничений.
5. Скопируем формулу, введенную в ячейку G8, в ячейки G9:G12.
6.В ячейку B13введем формулу: =СУММ(B8:B12), которая представляет шестое ограничение из приведенной системы ограничений.
7.Скопируем формулу, введенную в ячейку B13,в ячейкиC13:F13.
Внешний вид рабочего листа MS Office Excel 2003 с исходными данными для решения задачи о назначении представлен на рис. 2.7.
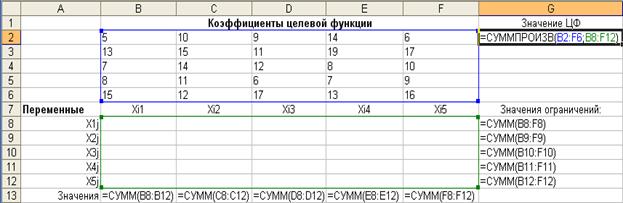
Рис. 2.7. Исходные данные для решения задачи о назначении
Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию главного меню: Сервис Þ Поиск решения.
После появления диалогового окна Поиск решенияследует выполнить следующие действия:
1.В поле с именем Установить целевую ячейку:ввести абсолютный
адрес ячейки $G$2.
2.Для группы Равной:выбрать вариант поиска решения – минимальному значению.
3.В поле с именем Изменяя ячейки:ввести абсолютный адрес диапазона ячеек $B$8:$F$12.
4.Задать первую группу ограничений, соответствующих первым 5 базовым ограничениям исходной постановки решаемой задачи о назначении. С этой целью выполнить следующие действия:
î в исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить;
îв появившемся дополнительном окне выбрать диапазон ячеек $G$8:$G$12,который должен отобразиться в поле с именем Ссылка на ячейку;
îв качестве знака ограничения из выпадающего списка выбрать равенство «=»;
îв качестве значения правой части ограничения ввести с клавиатуры число 1;
îдля добавления первой группы ограничений в дополнительном окне нажать кнопку с надписью Добавить.
5.Задать вторую группу ограничений, соответствующих оставшимся 5 базовым ограничениям исходной постановки решаемой задачи о назначении. С этой целью выполнить следующие действия:
îв исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить.
îв появившемся дополнительном окне выбрать диапазон ячеек $B$13:$F$13, который должен отобразиться в поле с именем Ссылка на ячейку;
îв качестве знака ограничения из выпадающего списка выбрать равенство «=»;
îв качестве значения правой части ограничения ввести с клавиатуры число 1;
îдля добавления второй группы ограничений в дополнительном окне нажать кнопку с надписью Добавить.
6.Добавить последнее ограничение на булевы значения переменных задачи. С этой целью выполнить следующие действия:
îв исходном диалоговом окне Поиск решениянажать кнопку с надписью Добавить;
îв появившемся дополнительном окне выбрать диапазон ячеек $B$8:$F$12,который должен отобразиться в поле с именем Ссылка на ячейку;
î в качестве знака ограничения из выпадающего списка выбрать строку «двоичн»;
îв качестве значения правой части ограничения в поле с именем Ограничение:оставить без изменения вставленное программой значение «двоичное»;
î для добавления в дополнительном окне нажать кнопку с надписью Добавить.
7.В окне дополнительных параметров поиска решения выбрать отметку Линейная модельиНеотрицательные значения.
Общий вид диалогового окна спецификации параметров мастера поиска решения представлен на рис. 2.8.
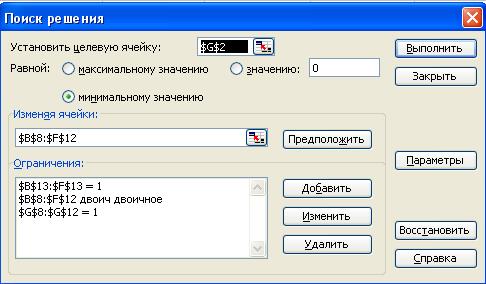
Рис. 2.8.Параметры мастера поиска решения и базовые ограничения
для задачи о назначении
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить.После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, приведенный на рис. 2.9.
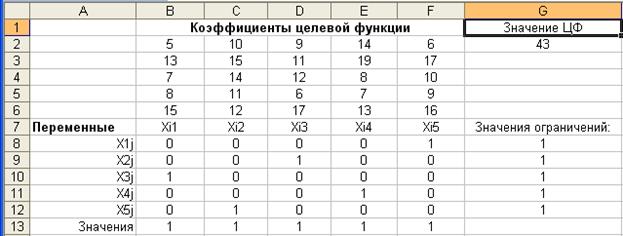
Рис. 2.9.Результат количественного решения задачи о назначении
Результатом решения рассматриваемой задачи о назначении являются найденные оптимальные значения переменных: х15 = 1, х23 = 1, х31 = 1, х44 = 1, х52 =1, остальные переменные равны 0. Найденному оптимальному решению соответствует минимальное значение целевой функции ¦opt = 43.
Анализ найденного решения показывает, что при замещении вакантных должностей в рассматриваемой фирме следует на должность менеджера назначить сотрудника Дмитриева, на должность программиста – Васильева, на должность бизнес-аналитика – Андреева, на должность маркетолога – Григорьева и, наконец, на должность руководителя проектов – Бубнова. При этом общие затраты на обучение и стажировку сотрудников составят 43 тыс. тенге.
Большинство целочисленных и комбинаторных типов задач, таких, как задача с неделимостями, задача коммивояжера, задача календарного планирования, принадлежит к разряду так называемых трудно решаемых. Это означает, что вычислительная сложность алгоритма их точного решения – зависимость числа элементарных операций (операций сложения или сравнения), необходимых для получения точного решения, от размерности задачи n – является экспоненциальной (порядка 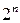 ), т.е. сравнимой по трудоемкости с полным перебором вариантов. В качестве n, например, для задачи с неделимостями служит число целочисленных переменных и число ограничений, для задачи коммивояжера – число городов (или узлов графа маршрутов), для задачи календарного планирования – число деталей и число станков. Такие задачи называют еще NP-трудными или NP-полными. Получение их точного решения не может быть гарантировано, хотя для некоторых задач данного типа существует эффективные методы, позволяющие находить точное решение даже при больших размерностях. Примером таких задач служит задача о ранце с булевыми переменными.
), т.е. сравнимой по трудоемкости с полным перебором вариантов. В качестве n, например, для задачи с неделимостями служит число целочисленных переменных и число ограничений, для задачи коммивояжера – число городов (или узлов графа маршрутов), для задачи календарного планирования – число деталей и число станков. Такие задачи называют еще NP-трудными или NP-полными. Получение их точного решения не может быть гарантировано, хотя для некоторых задач данного типа существует эффективные методы, позволяющие находить точное решение даже при больших размерностях. Примером таких задач служит задача о ранце с булевыми переменными.
Дата добавления: 2015-11-18; просмотров: 5819;
