ОПТИМАЛЬНОСТЬ БАЗИСНОГО РЕШЕНИЯ
Рассмотрим нахождение оптимального решения транспортной задачи методом потенциалов на конкретном примере.
На складах А1, А2, А3 имеются запасы продукции в количествах 90, 400, 100 т соответственно. Потребители В1, В2, В3 должны получить эти продукцию в количествах 140, 300, 160 т соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т продукции заданы матрицей (ден. ед.):
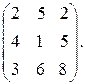
Проверим, является ли данная транспортная задача закрытой.
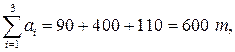
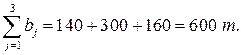
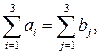
следовательно, данная транспортная задача закрытая. Найдем исходный опорный план по методу минимального тарифа.
Таблица 3.4
| Поставщики | Потребители | Запасы, ai | ||
| B1 | B2 | B3 | ||
| A1 | 90 | |||
| A2 | 300 | 100 | ||
| A3 | 50 | 60 | ||
| Потребности, bj | 600 = 600 |
Число занятых клеток в таблице равно 5, m + n – 1 = 3 + 3 – 1 = 5, т.е. условие невырожденности выполнено.
Стоимость перевозки при исходном опорном решении составляет:
Z1 = 90·2 + 300·1 + 100·5 + 50·3 + 60·8 = 1610 ден. ед.
Найденное исходный опорный план проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m + n действительных чисел αi и βj, удовлетворяющих условиям 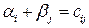 для занятых клеток
для занятых клеток 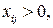 и
и 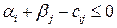 для свободных (незанятых) клеток.
для свободных (незанятых) клеток.
Числа αi и βj называют потенциалами. В распределительную таблицу добавляют строку βj и столбец αi.
Потенциалы αi и βj находят из равенства 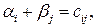 справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например α1 = 0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал αi, то βj = cij – αi, если известен потенциал βj, то αi = cij – βj.
справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, например α1 = 0, тогда остальные потенциалы определяются однозначно. Так, если известен потенциал αi, то βj = cij – αi, если известен потенциал βj, то αi = cij – βj.
Обозначим 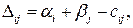 которую называют оценкой свободных клеток. Если все оценки свободных клеток
которую называют оценкой свободных клеток. Если все оценки свободных клеток 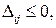 то опорный план является оптимальным. Если хотя бы одна из оценок
то опорный план является оптимальным. Если хотя бы одна из оценок 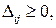 то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.
Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец αi и строку βj.
Таблица 3.5
| Поставщики | Потребители | Запасы, ai | Потенциал строк, αi | ||
| B1 | B2 | B3 | |||
| A1 | 2 90 | 5 | 2 | 90 | 0 |
| A2 | 4 | 1 300 | 5 100 | 400 | – 2 |
| A3 | 3 50 | 6 | 8 60 | 110 | 1 |
| Потребности, bj | 600 = 600 | ||||
| Потенциал столбцов, βj | 2 | 3 | 7 |
Полагаем α1= 0, запишем это значение в последнем столбце первой строки таблицы.
Рассмотрим занятую клетку первой строки, которая расположена в первом столбце (А1;В1), для нее выполняется условие α1 + β1 = с11 или 0 + β1 = 2, откуда β1 = 2. Это значение запишем в последней строке первого столбца таблицы. Далее надо рассматривать ту из занятых клеток таблицы, для которой один из потенциалов известен.
Рассмотрим занятую клетку (А3; В1): α3 + β1 = 3, где β1 = 2, откуда α3 = 1.
Для клетки (3, 3): α3 + β3 = 8, α3 = 1, β3 = 7.
Для клетки (2, 3): α2 + β3 = 5, α3 = 7, β2 = – 2.
Для клетки (2, 2): α2 + β2 = 1, α2 = – 2, β2 = 3.
Найденные значения потенциалов заносим в таблицу.
Вычисляем оценки свободных клеток:
Δ12 = α1 + β2 – с12 = 0 + 3 – 5 = – 2 < 0,
Δ13 = α1 + β3 – с13 = 0 + 7 – 2 = 5 > 0,
Δ21 = α2 + β1 – с21 = – 2 + 2 – 4 = – 4 < 0,
Δ32 = α3 + β2 – с32 = 1 + 3 – 6 = – 2 < 0.
Получили одну оценку Δ13 = 5 > 0, следовательно, исходный опорный план не является оптимальным и его можно улучшить.
Наличие положительной оценки свободной клетки (Δij > 0) при проверке опорного плана на оптимальность свидетельствует о том, что полученное решение не оптимально и для уменьшения значения целевой функции надо перейти к другому опорному решению. При этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. Свободная клетка становится занятой, а одна из ранее занятых клеток – свободной.
Для свободной клетки с Δij > 0 строится цикл (цепь, многоугольник), все вершины которого кроме одной находятся в занятых клетках; углы прямые, число вершин четное. Около свободной клетки цикла ставится знак (+), затем поочередно проставляют знаки (–) и (+). У вершин со знаком (–) выбирают минимальный груз, его прибавляют к грузам, стоящим у вершин со знаком (+), и отнимают от грузов у вершин со знаком (–). В результате перераспределения груза получим новое опорное решение. Это решение проверяем на оптимальность, и т.д. до тех пор, пока не получим оптимальное решение.
Рассмотрим переход от одного опорного решения к другому на заданном примере.
Строим цикл для клетки (А1; В3), имеющий положительную оценку. У вершин цикла ставим знаки (+) и (–) и записываем грузы:
– +

+ –
У вершин со знаком (–) выбираем минимальный груз, он равен 60. Его прибавляем к грузам, стоящим у положительных вершин, и отнимаем от грузов, стоящих у отрицательных вершин. Получаем новый цикл:
30 60

110 0
Новое опорное решение:
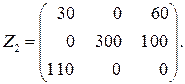
Проверим полученное решение на оптимальность. Для этого запишем его в распределительную таблицу, найдем потенциалы занятых и оценки свободных клеток (табл. 3.6).
Таблица 3.6
| Поставщики | Потребители | Запасы, ai | Потенциал строк, αi | ||
| B1 | B2 | B3 | |||
| A1 | 2 30 | 5 | 2 60 | 90 | 0 |
| A2 | 4 | 1 300 | 5 100 | 400 | 3 |
| A3 | 3 110 | 6 | 8 | 110 | 2 |
| Потреб–ти, bj | 600 = 600 | ||||
| Потенциал столбцов, βj | 2 | – 2 | 2 |
Имеем
Δ12 = – 7, Δ21 = 1 > 0, Δ32 = – 7, Δ33 = – 5.
Построим цикл для клетки с положительной оценкой Δ21 = 1:
– +

+ –
Произведем перераспределение грузов:
0 90

30 70
Получим новое решение, которое занесем в табл. 3.7. Проверим его на оптимальность.
Таблица 3.7
| Поставщики | Потребители | Запасы, ai | Потенциал строк, αi | ||
| B1 | B2 | B3 | |||
| A1 | 2 | 5 | 2 90 | 90 | 0 |
| A2 | 4 30 | 1 300 | 5 70 | 400 | 3 |
| A3 | 3 110 | 6 | 8 | 110 | 2 |
| Потребности, bj | 600 = 600 | ||||
| Потенциал столбцов, βj | 1 | – 2 | 2 |
Получим
Δ11 = – 1, Δ12 = – 1, Δ32 = – 6, Δ33 = – 4.
Все оценки свободных клеток отрицательные, следовательно, найденное решение оптимальное. Итак,
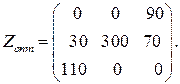
Стоимость транспортных расходов равна
Zmin = 90·2 + 30·4 + 300·1 + 70·5 + 110·3 = 1280 ден. ед.
По сравнению с исходным опорным планом транспортные расходы уменьшились на 1610 – 1280 = 330 ден. ед.
Альтернативный оптимум. Признаком наличия альтернативного оптимума в транспортной задаче является равенство нулю хотя бы одной из оценок свободных переменных в оптимальном решении (Хопт1). Сделав перераспределение грузов относительно клетки, имеющей Δij = 0, получим новое оптимальное решение (Хопт2), при этом значение целевой функции (транспортных расходов) не изменится. Если одна оценка свободных переменных равна нулю, то оптимальное решение находится в виде
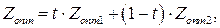
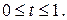
Дата добавления: 2015-11-18; просмотров: 1635;
