ТРАНСПОРТНАЯ МОДЕЛЬ

Транспортные модели (задачи) представляют специальный класс задач линейного программирования. Такие модели используются для разработки наиболее экономичных планов перевозки продукции одного вида из нескольких пунктов отправки в пункты назначения.

Транспортные модели также применяются при составлении расписаний, управлении запасами, управлении движением капиталов, назначении персонала и во многих других задачах подобного вида.

В свою очередь транспортные модели и их модификации представляют собой частный случай так называемых сетевых моделей, в рамках которых можно сформулировать и решить большое число практически важных задач, в частности, задачу нахождения наикратчайшего пути между двумя пунктами по существующей сети дорог.

Транспортную задачу и ее модификации можно решать симплексным методом. Однако специфика ограничений в этих задачах позволила разработать более эффективные вычислительные процедуры для их решения, в частности, метод потенциалов для транспортной задачи. По существу метод потенциалов воспроизводит все шаги симплекс-метода.

Транспортным задам присущи следующие особенности:

· распределению подлежат однородные ресурсы;

· условия задачи (ограничения) описываются только уравнениями;

· все переменные выражаются в одинаковых единицах измерения;

· во всех уравнениях коэффициенты при неизвестных равны единице;

· каждая неизвестная встречается только в двух уравнениях системы ограничений.

В общем виде транспортную задачу можно представить следующим образом: в m пунктах производства А₁, А₂, ..., А_m имеется однородный груз в количествах, соответственно, а₁, а₂, ..., а_m. Этот груз необходимо доставить в n пунктов назначения В₁, В₂, ..., В_m в количествах, соответственно, в₁, в₂,..., в_n. Стоимость перевозки 1 ед. груза (тариф) из пункта A_i в пункт B_j равна c_ij ден. ед.

Требуется составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребителей, и имеющий минимальную стоимость.

Транспортная задача имеет n + m уравнений (ограничений) с n´ m неизвестными.

В зависимости от соотношения между суммарными запасами груза и суммарными потребностями в нем, транспортные задачи могут быть закрытыми и открытыми.

Если сумма запасов груза равна суммарной потребности в нем, т.е.

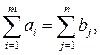
то транспортная задача называется закрытой.

Если сумма запасов груза не равна суммарной потребности в нем, т.е.

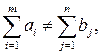
то транспортная задача называется открытой.

Решение транспортной задачи разбивается, как и симплексный метод, на следующие этапы:

· нахождение исходного опорного плана;

· проверка этого плана на оптимальность;

· переход от одного опорного плана к другому, пока не будет найдено оптимальное распределение поставок.