Аналитическая модель поверхности

Аналитической моделью называется описание поверхности математическими формулами:

z=f(x,y) – описание с помощью функции,

F(x,y,z)=0 – описание с помощью неявного уравнения.

Зачастую используется параметрическая форма описания поверхности:

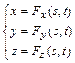
где s и t – параметры, которые изменяются в определенном диапазоне, а функции F_x, F_y и F_z определяют форму поверхности.

Преимущество параметрической формы заключается в легкости описания поверхностей, которые отвечают неоднозначным функциям, и замкнутых поверхностей.

Параметрическое описание можно задать таким образом, что формула не будет существенно изменяться (усложняться) при поворотах поверхности, и ее масштабировании.

В качестве примера рассмотрим аналитическое описание поверхности шара.

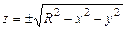— явная функция двух аргументов,

x2 + y2 + z2 -R2 = 0 — неявное уравнение,

x = R sin s cos t, y = R sin s sin t, z = R cos s — в параметрической форме.

Для описания сложных поверхностей часто используют сплайны. Сплайн – это специальная функция для аппроксимации отдельных фрагментов поверхности. Несколько сплайнов образуют модель сложной поверхности. Иными словами, сплайн – это тоже поверхность, но такая, для которой можно достаточно просто вычислять координаты ее точек. В трехмерной графике обычно используют кубические сплайны по двум основным причинам:

– третья степень – наименьшая из степеней, позволяющих описывать любую форму;

– при стыковке сплайнов можно обеспечить непрерывную первую производную – такая поверхность будет без изломов в местах стыка.

Сплайны, как правило, задают параметрически.

Рассмотрим одну из разновидностей сплайнов – сплайн Безье. В обобщенной форме (степени m*n):

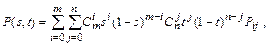
где P_ij – опорные точки-ориентиры, 0 £ s £ 1, 0 £ t £ 1, C_mⁱ и C_n^j – коэффициенты бинома Ньютона, которые рассчитываются по формуле

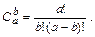
Кубический сплайн Безье соответствует значениям m=3, n=3. Для его определения необходимо 16 точек-ориентиров P_ij; коэффициенты C_mⁱ и C_n^j равны 1, 3, 3, 1 при i, j = 0, 1, 2, 3.

Аналитическая модель наиболее пригодна для многих операций анализа поверхностей.

Достоинства модели (с позиций КГ):

● легкость расчета координат каждой точки поверхности, нормали;

● небольшой объем данных для описания достаточно сложных форм.

Недостатки:

● сложность формул описания с использованием функций, которые медленно вычисляются на компьютере, снижают скорость выполнения операций отображения;

● невозможность в большинстве случаев применить данную форму описания непосредственно для изображения поверхности - поверхность отображается как многогранник, координаты вершин и граней которого рассчитываются в процессе отображения, что уменьшает скорость сравнительно с полигональной моделью описания.