Геометрические фракталы
Геометрическими названы фракталы, форма которых может быть описана как последовательность простых геометрических операций. Геометрические фракталы строятся на основе исходной фигуры – линии, полигона, полиэдра – путем ее дробления и выполнения аффинных и логических преобразований (объединения или исключения) полученных фрагментов.
 |
Метод построения фрактального объекта может быть как итерационным, так и рекурсивным, причем рекурсивный чаще бывает богаче возможностями и проще в программировании. Например, кривая Кох становится фракталом в результате бесконечного количества итераций, в ходе которых выполняется деление каждого отрезка прямой на три части. На средней части
отрезка строится правильный треугольник, затем процесс повторяется для каждого из полученных отрезков, кроме среднего (рис. 22).
Алгоритм основан на рекурсивном вызове процедуры для каждого из полученных отрезков. Аналогичный алгоритм используется при построении фрактального треугольника.
Вообще алгоритм построения кривой Кох можно применить к любому многоугольнику или ломаной линии, запустив алгоритм построения кривой Кох для каждого из составляющих фигуру отрезков (в приложении 2 содержится программа построения кривой Кох и фрактального треугольника с помощью этой процедуры).
Площадные фракталы
Строительными элементами площадных геометрических фракталов служат плоские полигоны, чаще всего трех- и четырехугольники.
Самым знаменитым фракталом этого класса является треугольник Серпинского, строящийся путем разбиения треугольника – не обязательно равностороннего – средними линиями на четыре подобных треугольника, исключения центрального и рекурсивного разбиения угловых треугольников до получения площадных элементов желаемого или минимально видимого разрешения.
Алгоритм построения треугольника Серпинского (рис. 23).
1. 
Внутри исходного треугольника выбирается центральная точка:
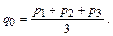
2. Задается число m итераций генерирования случайных точек.
3. В цикле для k от 1 до m:
– случайным образом выбирается номер n одной из вершин треугольника pn (генерируется случайное число в интервале от 1 до 3).
– вычисляется очередная точка qk в середине отрезка qk-1 pn:
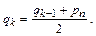
Благодаря выбору точки q0 внутри треугольника p1 p2 p3 центр отрезка q0 pn (точка q1) никогда не окажется внутри центрального треугольника, отмеченного на рисунке пунктиром. При достаточно большом числе итераций m генерируемые точки qk образуют случайный узор, предельная форма которого стремится к треугольнику Серпинского.
Следует отметить, что небольшое число начальных точек qk все-таки может попасть в запретные области. В частности, это случится при выборе точки q0 в центре треугольника p1 p2 p3 .
Аналогично треугольнику Серпинского может быть построена треугольная пирамида Серпинского.
Дата добавления: 2015-11-20; просмотров: 1095;