ВОПРОС 10. КЛАССИФИКАЦИЯ РЕЗЬБ. ГЕОМЕТРИЧЕСКИЕ ПАРАМЕТРЫ РЕЗЬБЫ.
Резьба ‑ выступы, образованные на основной поверхности винтов или гаек и расположенные по винтовой линии.
По форме основной поверхности различают цилиндрические и конические резьбы.
По направлению винтовой линии различают правую и левую резьбы.
По числу заходов различают однозаходную, двухзаходную и т. д. резьбы.
По форме профиля:
метрическая с треугольным профилем ‑ основная крепежная резьба;
трубная ‑ треугольная со скругленными вершинами и впадинами;
круглая;
резьба винтов для дерева;
прямоугольная;
трапецеидальная симметричная;
упорная.
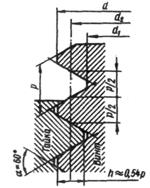
Геометрические параметры резьбы
d ‑ наружный (номинальный) диаметр;
d1 ‑ внутренний диаметр (d и d1одинаковы для винта и гайки, а зазоры во впадинах образуют за счет предельных отклонений размеров этих диаметров);
d2 ‑ средний диаметр (диаметр воображаемого цилиндра, образующая которого пересекает резьбу в таком месте, где ширина выступа равна ширине впадины);
h ‑ рабочая высота профиля, по которой соприкасаются боковые стороны резьб винта и гайки;
р ‑ шаг (расстояние между одноименными сторонами соседних профилей, измеренное в направлении оси резьбы);
р1 ‑ ход (поступательное перемещение образующего профиля за один оборот или относительное осевое перемещение гайки за один оборот).
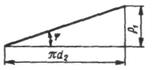Для однозаходной резьбы р1 = р; для многозаходной р1 = n·р, где n ‑ число заходов;
α ‑ угол профиля;
ψ ‑ угол подъема (угол подъема развертки винтовой линии по среднему диаметру);
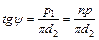
Все геометрические параметры резьб и допуски на их размеры стандартизованы.
ВОПРОС 11. ОПРЕДЕЛЕНИЕ МОМЕНТА ЗАВИНЧИВАНИЯ РЕЗЬБОВОЙ ПАРЫ.
Осевая сила F, действующая по стержню винта, уравновешивается реакцией гайки, распределенной по виткам резьбы. Эта реакция условно заменена сосредоточенной силой Fn, нормальной к линии профиля. При этом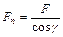 
и сила трения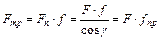 
где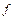 
‑ действительный коэффициент трения;
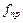‑ приведенный, коэффициент трения в резьбе:
Если винт нагружен осевой силой F, то для завинчивания гайки к ключу необходимо приложить момент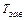 
, а к стержню винта ‑ реактивный момент 
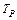, который удерживает стержень от вращения. При этом можно записать:
(*)
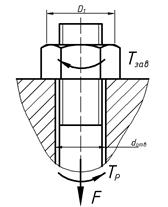
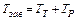где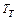 
‑ момент сил трения на опорном торце гайки;
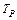‑ момент сил трения в резьбе.
Радиус сил трения на опорном торце гайки принимают равным среднему радиусу этого торца или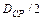 
. При этом
(**)
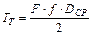где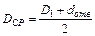 
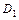‑ наружный диаметр опорного торца гайки;
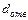‑ диаметр отверстия под винт;
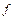‑ коэффициент трения на торце гайки.
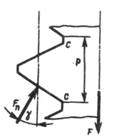
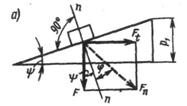
Момент сил трения в резьбе определим, рассматривая гайку как ползун, поднимающийся по виткам резьбы, как по наклонной плоскости. По известной теореме механики, учитывающей силы трения, ползун находится в равновесии, если равнодействующая Fп системы внешних сил отклонена от нормали n ‑ n на угол трения φ.
В нашем случае внешними являются осевая сила F и окружная сила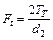 
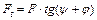
или
(***)
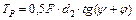где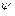 
‑ угол подъема резьбы;
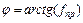‑ угол трения в резьбе;
Подставляя (**) и (***) в формулу (*), найдем искомую зависимость:
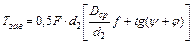
При отвинчивании гайки окружная сила F, и силы трения меняют направление. При этом получим
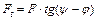
Момент отвинчивания с учетом трения на торце гайки, по аналогии с формулой (1.6),
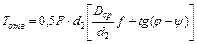
ВОПРОС 12. САМОТОРМОЖЕНИЕ И КПД РЕЗЬБОВОЙ ПАРЫ. РАСЧЁТ РЕЗЬБЫ НА ПРОЧНОСТЬ.
Условие самоторможения можно записать в виде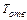 
> 0. Рассматривая самоторможение только в резьбе без учета трения на торце гайки, получим
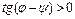или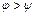 
Для крепежных резьб угол подъема 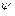находится в пределах 2°30'…3°30', а угол трения 
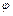изменяется в зависимости от коэффициента трения в пределах от 6° до 16°. Таким образом, все крепежные резьбы — самотормозящие. Ходовые резьбы выполняют как самотормозящими, так и несамотормозящими.
КПД (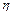 
) винтовой пары можно вычислить по отношению работы, затраченной на завинчивание гайки без учета трения, к той же работе с учетом трения. Работа завинчивания равна произведению момента завинчивания на угол поворота гайки. Так как углы поворота равны и в том и в другом случае, то отношение работ равно отношению моментов 
/ 
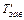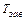,в котором 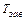определяется по формуле, а 
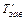‑ по той же формуле, но пр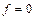и 
и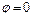 
.
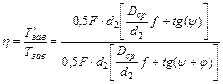
Учитывая потери только в резьбе ( 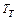= 0), найдем КПД собственно винтовой пары:
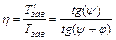
Дата добавления: 2015-09-14; просмотров: 1306;