Фракталы на основе метода IFS

Эту группу составляют фракталы, которые генерируются согласно методу "систем итеративных функций" – IFS (Iterated Functions Systems).

Данный метод может быть описан как последовательный итеративный расчет координат новых точек в пространстве:

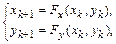
где F_x и F_y – функции преобразования координат, например аффинного преобразования. Эти функции и определяют форму фрактала. В случае аффинного преобразования необходимо найти соответствующие числовые значения коэффициентов. Примером такого фрактала является построение изображения листа папоротника (рис. 24).

Для начала итераций необходимо задать стартовые координаты линии – точки 1 и 2. На каждом шаге итераций рассчитываются координаты других точек.

Точка 3 получается поворотом точки 2 на угол a относительно центра в точке 1:

x3=(x2-x1)cosa-(y2-y1)sina+x1,

y3=(x2-x1)sina+(y2-y1)cosa+y1.

Если a=0, то ствол и все ветви прямые.

Находим точку 4. От нее будут распространяться ветви. Пусть соотношение длин отрезков 1-4 и 1-3 равно k (0<k<1). Тогда координаты точки 4: x4=x1(1-k)+kx3, y4=y1(1-k)+ky3.

Задаем длину и угол наклона ветвей, которые выходят из точки 4.

Найдем координаты точки 5: параметр k1– соотношение длин отрезков 4-5 и 4-3 (0<k1<1):

x5=x4(1-k1)+k1x3,

y5=y4(1-k1)+k1y3.

Точка 6 получается поворотом точки 5 относительно точки 4 на угол b, а точка 7 – на угол (-b):

x6=(x5-x4)cosb-(y5-y4)sinb+x4;

y6=(x5-x4)sinb+(y5-y4)cosb+y4;

x7=(x5-x4)cosb+(y5-y4)sinb+x4;

y7=-(x5-x4)sinb+(y5-y4)cosb+y4.

После расчета опорных точек на каждом шаге рисуется отрезок 1-4. В зависимости от номера итерации цвет отрезка можно изменять.

Таким образом, фрактал задается как последовательность аффинных преобразований координат точек. Величины a, b, k, k1 – это параметры, которые описывают вид фрактала в целом. Они представляют собой константы на протяжении всего итеративного процесса. Это дает возможность в итерациях использовать только операции сложения, вычитания и умножения, если вычислить заранее значения:

A=cosa; B=sina; C=(1-k); D=k;

E=1-k1; F=k1; G=cosb; H=sinb.

Опишем рекурсивный алгоритм в виде процедуры ШАГ.

ШАГ(x1, y1, x2, y2, num)

Если (x1-x2)²+(y1-y2)²>lmin, то

Вычисляем координаты точек 3-7:

x3=(x2-x1)A ­- (y2-y1)B + x1

y3=(x2-x1)B + (y2-y1)A + y1

x4=x1C + x3D

y4=y1C + y3D

x5=x4E + x3F

y5=y4E + y3F

x6=(x5-x4)G - (y5-y4)H + x4

y6=(x5-x4)H + (y5-y4)G + y4

x7=(x5-x4)G + (y5-y4)H + x4

y7=-(x5-x4)H + (y5-y4)G + y4

Рисуем отрезок (x1, y1 - x4, y4)

ШАГ(x4, y4, x3, y3, num)

ШАГ(x4, y4, x6, y6, num+1)

ШАГ(x4, y4, x7, y7, num+1)

Для того чтобы нарисовать фрактал, необходимо вызвать процедуру ШАГ, установив соответствующие значения ее аргументов: ШАГ(x1,y1,x2,y2,0). Параметр num показывает степень детализации расчета дерева. Это значение можно использовать для прекращения итеративного процесса.

Завершение циклов итерации в нашем алгоритме происходит тогда, когда длина ветви становится меньше некоторой величины lmin.