Проецирование трехмерных объектов на картинную плоскость

Важнейшей операцией при визуализации трехмерной графики является проектирование, поскольку изображение строится на плоской поверхности экрана.

Проектирование – это преобразование, ставящее в соответствие точкам трехмерного пространства точки на некоторой плоскости, называемой картинной.

В компьютерной графике используются два основных вида проектирования: параллельное и перспективное.

Параллельное проектирование (рис. 25) Пусть уравнение плоскости задано в виде n_xx + n_yy + n_zz + d = 0, где x, y, z – координаты произвольной точки p этой плоскости. Уравнение плоскости может быть записано в виде скалярного произведения векторов: n=(n_x, n_y, n_z) и p=(x, y, z): (n, p) + d = 0.

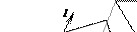Рассмотрим плоскость π: (n, p) + d = 0 в трехмерном пространстве, на которую будет осуществляться проектирование (картинную плоскость). Пусть задан вектор l, вдоль которого будет осуществляться проектирование. При этом будем считать, что (l, n)≠ 0.

Для нахождения проекции произвольной точки q на плоскость π проведем через точку q прямую с направляющим вектором l. Точка пересечения этой прямой с плоскостью π – q_пр – является проекцией точки q на плоскость π вдоль направления l.

Координаты произвольной точки q' прямой, проходящей через точку q и имеющей направляющий вектор l:

q' = q + tl, tÎR.

Тогда параметр t точки пересечения этой прямой и плоскости π можно найти, подставив уравнение прямой в уравнение плоскости:

(q + tl, n) + d = 0.

Отсюда получаем

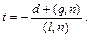
Зная t, можно найти проекцию точки q по формуле q_пр = q + tl.

Так как параллельное преобразование является аффинным, то его можно задать при помощи матрицы однородного преобразования.

Приведем матрицу канонического параллельного проектирования, осуществляемого на плоскость Oxy вдоль оси Oz.

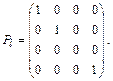
Несмотря на свою простоту, параллельное проектирование обычно малоприменимо для визуализации сложных трехмерных сцен.

Перспективное проектирование (рис. 26). Рассмотрим картинную плоскость π: (n, p) + d = 0 . Пусть задана точка c, которую будем называть центром проектирования. Тогда перспективной проекцией точки q назовем точку q_пр пересечения плоскости π с лучом, выходящим из c и проходящим через q при условии, что точка q лежит в положительном полупространстве относительно плоскости π.

Пусть проекцией точки q является точка q_пр. В силу того, что q_пр лежит на отрезке [q, c], справедлива формула

q_пр = (1 - t)c + tq, t Î [0, 1].

Тогда из условия принадлежности проекции плоскости получаем

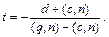
Как видно из этой формулы, перспективное преобразование не является аффинным (принадлежит классу дробно-линейных преобразований). Тем не менее, его также можно записать при помощи матрицы однородного преобразования.

Выпишем каноническое уравнение перспективного преобразования. Пусть центр проектирования равен (0, 0, -1)^Т, а картинная плоскость задается уравнением z = 1.

Тогда проекцией произвольной точки q = (x, y, z) будет точка q_пр=(x/(z+1), y/(z+1),1)². Это преобразование осуществляется при помощи матрицы:

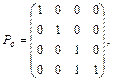
поскольку

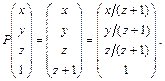
Таким образом, как произвольное аффинное преобразование, так и параллельное и перспективное проектирование могут быть записаны при помощи матриц однородных преобразований.