Закрашивание поверхностей
Рассмотрим методы закрашивания объектов, моделируемых многогранниками и полигональными сетками. Они основаны на моделях отражения света.
Зеркальное отражение. Угол между нормалью и падающим лучом равен углу между нормалью и отраженным лучом. Оба луча и нормаль располагаются в одной плоскости (рис. 27).
Поверхность считается идеально зеркальной, если на ней отсутствуют какие-либо неровности, шероховатости. Собственного цвета такая поверхность не имеет. Световая энергия падающего
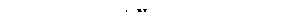 |
луча отражается только по линии отраженного луча. Какое-либо рассеяние в стороны от этой линии отсутствует. В природе, вероятно, нет идеально гладких поверхностей, поэтому полагают, что если глубина шероховатостей существенно меньше длины волны излучения, то рассеяние не наблюдается. Для видимого спектра можно принять, что глубина шероховатостей поверхности зеркала должна быть существенно меньше 0,5 мкм.
Если поверхность зеркала отполирована неидеально, то наблюдается зависимость интенсивности отраженного света от длины волны: чем больше длина волны, тем лучше отражение. Например, красные лучи отражаются сильнее, чем синие.
При наличии шероховатостей имеется зависимость интенсивности отраженного света от угла падения. Отражение света максимально для углов падения луча, близких к 90°.
Падающий луч, попадая на слегка шероховатую поверхность реального зеркала, порождает не один отраженный луч, а несколько лучей, рассеиваемых по различным направлениям. Зона рассеивания зависит от качества полировки и может быть описана некоторым законом распределения. Как правило, форма зоны рассеивания симметрична относительно линии идеального зеркально отраженного луча. К числу простейших, но достаточно часто используемых относится эмпирическая модель распределения Фонга, согласно которой интенсивность зеркально отраженного излучения пропорциональна (cos a)p, где a – угол отклонения от линии идеально отраженного луча. Показатель p находится в диапазоне от 1 до 200 и зависит от качества полировки. Соотношение можно записать следующим образом:
Is = I Ks cos pa,
где I – интенсивность излучения источника; Ks – коэффициент пропорциональности.
Диффузное отражение. Этот вид отражения присущ матовым поверхностям. Матовой можно считать такую поверхность, размер шероховатостей которой уже настолько велик, что падающий луч рассеивается равномерно во все стороны.
Диффузное отражение описывается законом Ламберта, согласно которому интенсивность отраженного света пропорциональна косинусу угла между направлением на точечный источник света и нормалью к поверхности:
Id = I Kd cos q,
где I – интенсивность источника света; Kd – коэффициент, который учитывает свойства материала поверхности. Значение Kd находится в диапазоне от 0 до 1.
Интенсивность отраженного света не зависит от расположения наблюдателя.
Матовая поверхность имеет свой цвет. Наблюдаемый цвет определяется комбинацией собственного цвета поверхности и цвета излучения источника света.
Поскольку в природе не существует идеально зеркальных или полностью матовых поверхностей, то при изображении объектов средствами КГ обычно моделируют сочетание зеркального и диффузного рассеивания в пропорции, характерной для конкретного материала. В этом случае модель отражения записывают в виде суммы диффузного и зеркального компонентов:
Iотр = I (Kd cos q + Ks cos pa),
где константы Kd, Ks определяют отражательные свойства материала.
Согласно этой формуле интенсивность отраженного света равна нулю для некоторых углов q и a. Однако в реальных сценах обычно нет полностью затемненных объектов, следует учитывать фоновую подсветку, освещение рассеянным светом, отраженным от других объектов. В таком случае интенсивность может быть эмпирически выражена следующей формулой:
Iотр = Ia Ka + I (Kd cos q + Ks cos pa),
где Ia – интенсивность рассеянного света, Ka – константа, определяющая рассеиваюшие свойства поверхности.
Следует учесть тот факт, что энергия от точечного источника света уменьшается пропорционально квадрату расстояния. Использования такого правила вызывает определенные сложности, поэтому на практике часто реализуют модель, выражаемую эмпирической формулой
Iотр = Ia Ka + I (Kd cos q + Ks cos pa)/(R + k),
где R – расстояние от центра проекции до поверхности, k – константа, подбираемая эмпирически.
Определение цвета закрашивания точек объектов в соответствии с описанной моделью. Наиболее просто выполняется расчет в градациях серого цвета (например, для белого источника света и серых объектов). В данном случае интенсивность отраженного света соответствует яркости.
Сложнее обстоит дело с цветными источниками света, освещающими цветные поверхности. Например, для модели RGB составляются три формулы расчета интенсивности отраженного света для различных цветовых компонентов. Коэффициенты Ka и Kd различны – они выражают собственный цвет поверхности. Поскольку цвет отраженного зеркального луча равен цвету источника, то коэффициент Ks будет одинаковым для всех компонентов цветовой модели. Цвет источника света выражается значениями интенсивности I для соответствующих цветовых компонентов.
Метод Гуро
Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения числа граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней – такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить число граней, что приводит к существенному замедлению визуализации – чем больше граней, тем меньше скорость рисования объектов.
Метод Гуро основывается на идее закрашивания каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней.
Закрашивание граней по методу Гуро осуществляется в четыре этапа.
1. Вычисляются нормали к каждой грани.
2. Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 28).
3. На основе нормалей в вершинах вычисляются значения интенсивности в вершинах согласно выбранной модели отражения света.
4. 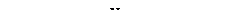 Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.
Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.
Вектор нормали в вершине (a) равен: Na = (N1 + N2 + N3) / 3.
Интерполированные значения интенсивности отраженного света в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно определять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 29).
 |
Интерполированная интенсивность I в точке (X, Y) определяется исходя из пропорции
(I - I1) / (X - X1) = (I2 - I1) / (X2 - X1).
Отсюда I = I1 + (I2 - I1)(X - X1) / (X2 - X1).
Значения интенсивностей I1 и I2 на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах:
(I1 - Ib) / (Y - Yb) = (Ic - Ib) / (Yc - Yb)
(I2 - Ib) / (Y - Yb) = (Ia - Ib) / (Ya - Yb)
или
I1 = Ib + (Ic - Ib)(Y - Yb) / (Yc - Yb)
I2 = Ib + (Ia - Ib)(Y - Yb) / (Ya - Yb)
Метод Фонга
Метод Фонга аналогичен методу Гуро, но при его использовании для определения цвета в каждой точке интерполируются не интенсивности отраженного света, а векторы нормалей (рис. 30).
 |
1. Определяются нормали к граням.
2. По нормалям к граням определяются нормали в вершинах.
3. В каждой точке закрашиваемой грани определяется интерполированный вектор нормали.
4. По направлению векторов нормали определяется цвет точек грани в соответствии с выбранной моделью отражения света.
Рассмотрим, как можно получить вектор нормали в каждой точке грани. Для интерполяции будем оперировать векторами N'a, N'b и N'c, исходящими из центра координат плоскости проецирования и параллельными соответствующим нормалям Na, Nb и Nc в вершинах a, b и c.
Сначала найдем N'1 и N'2:
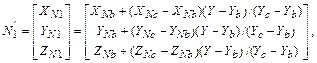
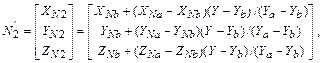
где XNa, YNa, ZNa, XNb, YNb, ZNb, XNc, YNc, ZNc – координаты векторов N'a, N'b и N'c.
Теперь найдем координаты вектора N':
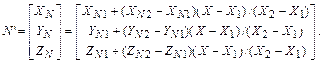
Вектор N' параллелен вектору N для нормали в точке (X, Y), поэтому его можно использовать для расчета отражения света так же, как и вектор нормали N.
Метод Фонга сложнее метода Гуро. Для каждой точки (пиксела) поверхности необходимо выполнять намного больше вычислительных операций (рис. 31). Тем не менее он дает значительно лучшие результаты, в особенности при имитации зеркаль
 |
ных поверхностей.
Дата добавления: 2015-11-20; просмотров: 2289;
