ЭКОНОМИЧЕСКИЙ АНАЛИЗ ТРАНСПОРТНЫХ ЗАДАЧ
Проведем экономический анализ задачи на конкретном примере.
Пример.Три торговых склада могут поставлять некоторое изделие в количестве 9, 4 и 8 т. Величины спроса трех магазинов розничной торговли на это изделие равны 3, 5 и 6 т.
Какова минимальная стоимость транспортировки от поставщиков к потребителям? Провести анализ решения при условии, что единичные издержки транспортировки в ден. ед. даны в матрице
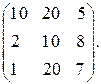
Решение. Запасы складов: 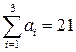 т, потребности магазинов:
т, потребности магазинов: 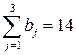 т; так как
т; так как 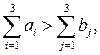 имеем открытую задачу. Введем фиктивный магазин со спросом b4ф = 21 – 14 = 7 т. Тариф фиктивного потребителя В4ф примем равным наибольшему из всех транспортных тарифов – 20 ден. ед. (табл. 3.8).
имеем открытую задачу. Введем фиктивный магазин со спросом b4ф = 21 – 14 = 7 т. Тариф фиктивного потребителя В4ф примем равным наибольшему из всех транспортных тарифов – 20 ден. ед. (табл. 3.8).
Таблица 3.8
| Поставщики | Потребители | Запасы, ai | Потенциал строк, αi | |||
| B1 | B2 | B3 | B4ф | |||
| А1 | 0 | |||||
| А2 | – 10 | |||||
| А3 | 0 | |||||
| Потреб–ти, bj | ||||||
| Потенциалы βj | 1 | 20 | 5 | 20 |
Оценки свободных клеток:
Δ11 = – 9, Δ21 = – 11, Δ23 = – 13, Δ24 = – 10, Δ32 = 0, Δ33 = – 2,
Δ34 = 0.
Оценки Δ32 = Δ34 = 0, задача имеет альтернативный оптимум, и одно из решений имеет вид
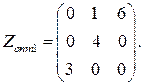
Минимальная стоимость транспортных расходов
Zопт1 = 93 ден. ед.
Итоговое распределение перевозок, а также значения оценок свободных клеток, которые называют теневыми ценами (двойственные оценки), можно использовать при проведении экономического анализа. Теневая цена показывает, на сколько увеличится общая стоимость транспортных расходов, если в пустую клетку поместить одно изделие. Например, если придется осуществить перевозку одного изделия с торгового склада А2 в розничный магазин В3, то увеличение стоимости составит 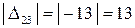 ден. ед., что больше, чем тариф груза клетки (А2; В3), равный 8 ден. ед. Дополнительное увеличение стоимости транс-портных расходов появляется в связи с перераспределением перевозок. Составим цикл распределения перевозок с помещением груза в пустую клетку (А2; В3):
ден. ед., что больше, чем тариф груза клетки (А2; В3), равный 8 ден. ед. Дополнительное увеличение стоимости транс-портных расходов появляется в связи с перераспределением перевозок. Составим цикл распределения перевозок с помещением груза в пустую клетку (А2; В3):

 + – 5 2
+ – 5 2
– + 0 4
В клетку (А2; В3) помещаем груз 4 т, в (А1; В3) – 2 т, в (А1; В2) – 5 т, в (А2; В2) вместо 4 т – пустая клетка.
Изменение расходов составит 4·20 – 4·10 + 4·8 – 4·5 = 72 ден. ед. или на одно изделие 72 : 4 = 13 ден. ед.
Если теневая цена клетки равна нулю (Δ32 = 0), то задача имеет альтернативный оптимум. Перераспределим грузы относительно клетки (А3; В2):
– + 0 3
 |  |
+ – 1 4
Еще одно оптимальное решение задачи имеет вид
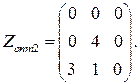
Минимальная стоимость транспортных расходов Zопт2 = 93 ден. ед.
Аналогичный анализ можно провести и по остальным свободным клеткам.
Теневые цены свободных клеток можно использовать в качестве индикаторов изменений стоимости транспортировки одного изделия или тарифа.
Например, теневая цена пустой клетки (А3; В3) равна 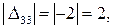 а фактическая цена транспортировки одного изделия – 7 ден. ед. Следовательно, для того чтобы использование данной клетки в распределении перевозок привело к снижению общих транспортных расходов, чтобы тариф этой клетки был бы не более 7 – 2 = 5 ден. ед.
а фактическая цена транспортировки одного изделия – 7 ден. ед. Следовательно, для того чтобы использование данной клетки в распределении перевозок привело к снижению общих транспортных расходов, чтобы тариф этой клетки был бы не более 7 – 2 = 5 ден. ед.
Приведем стоимостный анализ изменений в занятых клетках. При снижении тарифа увеличение числа изделий в данной клетке выгодно. Если же тарифы занятых клеток возрастают, то при достижении ими определенного значения использование этой клетки является нежелательным и необходимо произвести перераспределение грузов.
В качестве примера определим допустимые изменения тарифа занятой клетки (А1; В3). Тариф клетки равен 5 ден. ед. за одно изделие. Уменьшение этой величины не повлияет на объем перевозок, так как указанное количество изделий в клетке удовлетворяет всю потребность магазина 3.
Если тариф клетки (А3; В1) становится больше 5 ден. ед., то при составлении циклов будет задействована пустая клетка (А2; В3) с 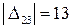 или (А3; В3) с
или (А3; В3) с 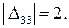 В обоих циклах клетка (А1; В3) будет иметь знак (–) и любое увеличение тарифа повлечет снижение теневой цены пустой клетки (А2; В3) или (А3; В3).
В обоих циклах клетка (А1; В3) будет иметь знак (–) и любое увеличение тарифа повлечет снижение теневой цены пустой клетки (А2; В3) или (А3; В3).
Изменение объема перевозок будет иметь место в случае, если тариф клетки (А1; В3) возрастет более чем на 2 ден. ед. и превысит 7 ден. ед. При этом теневая цена клетки (А3; В3) станет положительной и окажется невыгодным использование клетки (А1; В3).
Таким образом, для получения оптимального распределения перевозок тариф клетки (А1; В3) должен изменяться в диапазоне от 0 до 7 ден. ед. Внутри указанного промежутка происходит лишь изменение общей стоимости транспортных расходов, а распределение перевозок не меняется.
Дата добавления: 2015-11-18; просмотров: 1353;
