ЗАДАЧИ С БУЛЕВЫМИ ПЕРЕМЕННЫМИ
Частным случаем задачи целочисленных переменных являются задачи, в результате решения которых искомые переменные хj могут принимать не любые значения, а только одно из двух: либо 0, либо 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми.
В задачах с булевыми переменными могут быть выполнены все виды анализа. С точки зрения выполнения вариантного анализа для задач с булевыми переменными наибольший практический интерес представляет структурный анализ, под которым понимаем поиск оптимального решения при различных ограничениях.
Применение булевых переменных дает возможность накладывать на решаемую задачу целый ряд логических условий типа «если..., то...», например:
îесли в оптимальное решение МОЖЕТ входить один вариант ИЛИ другой (вместе они включены быть не могут), то в ограничениях ставится знак равенства:
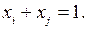
îесли в оптимальное решение МОЖЕТ входить (или не входить) один вариант И другой, то в ограничениях ставится знак неравенства:
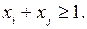
îв том случае, когда при принятии i-го варианта ДОЛЖЕН входить j-й, следует записать
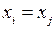
или
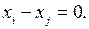
Таким образом, если накладывается условие ДОЛЖЕН, то в ограничениях ставится знак равенства, если МОЖЕТ – знак неравенства.
îаналогично можно записать логические условия для трех вариантов. Так, если в случае принятия k-го варианта должен быть принят либо вариант i, либо j, условие записывается так:
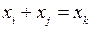
или
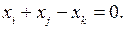
С помощью булевых переменных решаются разнообразные по содержанию задачи, связанные, например, с процессами выбора различных вариантов и дискретного программирования.
Экстремальные комбинаторные задачи.Задачи данного класса, называемые также задачами выбора, состоит в отыскании среди конечного множества альтернатив одной, которой отвечает экстремальное значение принятой целевой функции.
Задачи выбора вариантов.В общем случае математическая модель задачи выбора вариантов записывается следующим образом:
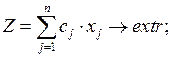
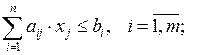 (2.3)
(2.3)
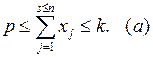
В данной системе ограничение (а) может учитывать самые разнообразные условия и требования, некоторые из которых приведены выше. Особенности решения данной задачи проиллюстрируем на решении следующего примера.
Чтобы получить прибыль, нам необходимы материальные и трудовые ресурсы, при этом возможны четыре варианта расхода ресурсов и получения прибыли (табл. 2.3). Требуется выбрать такие варианты, чтобы суммарная прибыль была максимальной при условии, чтобы общее число принятых вариантов k не превышало трех (k ≤ 3).
Таблица 2.3
Исходные данные задачи
| Показатели | Варианты | Наличие ресурса | |||
| Прибыль | – | ||||
| Ресурсы: | |||||
| материальные | |||||
| трудовые |
Принимаем, что
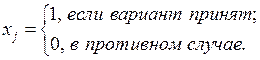
Тогда математическая модель задачи будет иметь вид:
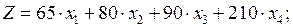
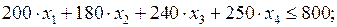 (2.4)
(2.4)
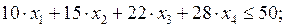
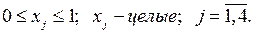
Задача коммивояжера– классический пример задачи выбора оптимального маршрута. Формулируется она следующим образом. Пусть имеется n городов. Выезжая из некоторого города, коммивояжер должен объехать все города, посетив каждый из них только один раз, и вернуться в исходный город. Таким образом, маршрут коммивояжера представляет собой цикл. Известны расстояния между любой парой городов. Требуется найти маршрут наименьшей длины.
Пусть 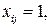 если коммивояжер переезжает из города i непосредственно в город j, и
если коммивояжер переезжает из города i непосредственно в город j, и 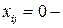 в противном случае. Обозначим через cij расстояние между городами i и j (чтобы избежать бессмысленных значений
в противном случае. Обозначим через cij расстояние между городами i и j (чтобы избежать бессмысленных значений 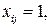 предполагается, что
предполагается, что 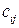 достаточно большому числу).
достаточно большому числу).
Тогда функция цели имеет вид:
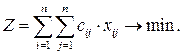 (2.5)
(2.5)
Определим ограничения задачи. Если коммивояжер из каждого города выезжает только один раз, то
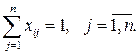 (2.6)
(2.6)
Аналогично, если коммивояжер въезжает в каждый город только один раз, то
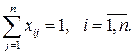 (2.7)
(2.7)
Чтобы обеспечить вхождение в цикл n городов, имеем ограничение
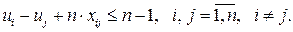 (2.8)
(2.8)
Здесь 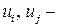 произвольные действительные числа.
произвольные действительные числа.
Наконец,
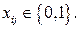 (2.9)
(2.9)
Ясно, что полученная задача (2.5) – (2.9) есть задача целочисленного линейного программирования.
Общая задача календарного планирования формулируется следующим образом. Имеется n станков (машин), на которых требуется обработать m деталей. Заданы маршруты (в общем случае различные) обработки каждой детали на каждом из станков или группе станков. Задана также продолжительность операций обработки деталей. Предполагается, что одновременно на станке можно обрабатывать не более одной детали. Требуется определить оптимальную последовательность обработки. Критерием оптимальности могут выступать продолжительность обработки всех деталей, суммарные затраты на обработку, общее время простоя станков и др. Существует огромное число постановок данной задачи, учитывающих конкретные условия производства.
Один из представителей задач данного типа – так называемая задача о ранце. Имеется n предметов. Предмет j 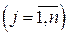 обладает весом
обладает весом 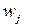 и полезностью cj. Пусть b – общий максимально допустимый вес предметов, которые можно положить в ранец. Требуется выбрать предметы таким образом, чтобы их общий вес не превышал максимально допустимый и при этом суммарная полезность (ценность) содержимого ранца была максимальной. Пусть
и полезностью cj. Пусть b – общий максимально допустимый вес предметов, которые можно положить в ранец. Требуется выбрать предметы таким образом, чтобы их общий вес не превышал максимально допустимый и при этом суммарная полезность (ценность) содержимого ранца была максимальной. Пусть 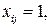 если предмет положен в ранец, и
если предмет положен в ранец, и 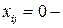 в противном случае. Математическая формулировка задачи имеет вид
в противном случае. Математическая формулировка задачи имеет вид
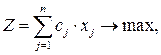
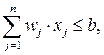
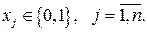
К классу экстремальных комбинаторных задач принадлежит также линейный и нелинейный варианты задач о назначениях.
Задача о назначениях.В процессе управления производством зачастую возникают задачи назначения исполнителей на различные виды работ, например, подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложений между различными проектами научно-технического развития и др.
Задачу о назначениях можно сформулировать следующим образом. Имеется n конечное число видов работ, которые могут быть выполнены n потенциальными кандидатами. При этом каждого кандидата можно назначать на выполнение только одной работы, а каждая работа, в свою очередь, должна выполняться только одним кандидатом. Известна эффективность выполнения каждой работы любым из потенциальных кандидатов. Требуется распределить всех кандидатов по работам так, чтобы общая эффективность выполнения всех работ была наибольшей. Оценочной функцией в данной задаче является общая эффективность выполнения всех работ, а ограничениями служат дополнительные условия на выполнение каждой работы только одним кандидатом и участие каждого кандидата в выполнении только одной работы.
Классическая задача о назначении – это симметричная задача, когда общее число видов работ равно количеству потенциальных кандидатов. В противном случае задача о назначениях называется несимметричной. Оба варианта этой задачи относятся к классу задач булева программирования.
Введем в рассмотрение следующие булевы переменные: 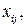 которые будут соответствовать назначению кандидатов на выполнение работ. В этом случае резонно предположить, что
которые будут соответствовать назначению кандидатов на выполнение работ. В этом случае резонно предположить, что 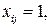 если i-й кандидат назначается на выполнение j-й работы, и
если i-й кандидат назначается на выполнение j-й работы, и 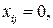 если i-й кандидат не назначается на выполнение j-й работы. Тогда математическая постановка задачи о назначениях может быть сформулирована следующим образом:
если i-й кандидат не назначается на выполнение j-й работы. Тогда математическая постановка задачи о назначениях может быть сформулирована следующим образом:
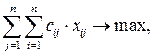
 (2.10)
(2.10)
где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств:
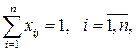 (2.11)
(2.11)
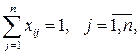 (2.12)
(2.12)
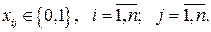 (2.13)
(2.13)
В математической постановке задачи о назначении (2.10) – (2.13) ограничение (2.11) соответствует требованию назначения каждого кандидата на выполнение только одной работы, а ограничение (2.12) – требованию выполнения каждой работы только одним кандидатом. Общее число булевых переменных задачи о назначении равно n2. При решении практических задач о назначении с помощью программы MS Excel особенности симметричной и несимметричной задач можно не принимать во внимание.
Если вместо эффективности выполнения работ кандидатами рассматриваются затраты, связанные с назначением кандидатов на выполнение работ, то исходная задача о назначении будет соответствовать задаче минимизации целевой функции (2.10). В итоге задача о назначении формируется как задача поиска оптимального назначения, которому соответствует минимум затрат на выполнение работ кандидатами. При этом ограничения задачи (2.11) – (2.13) остаются без изменения.
Дата добавления: 2015-11-18; просмотров: 3601;
